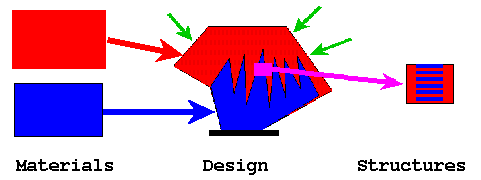

What kind of structures show optimal effective properties? The answer depends on the feature one wants to optimize.The picture illustrates concepts of structural optimization.
- The problem of design asks for a layout of several materials within the designed body in order to maximize an integral characteristics.
- As a rule, an optimal design is made from optimal composites: fine scale alternating subdomains of different materials. In order to make optimal constructions one needs to understand properties of composites with extremal properties.
| Laminate: maximal conductivity among layers | 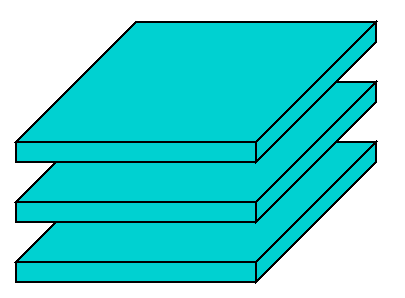 |
| Laminate: minimal conductivity across layers |
 |
| Coated spheres: minimal (or maximal) isotropic conductivity |  |
| Second-rank laminate: maximal (or minimal) conductivity in a direction
if the conductivity in an orthogonal direction is fixed. (a generalization
of coated shperes).
|
 |
| Elasticity: some structural optimization problems, requirements to structures, and the math. formulations | |||
| Maximal stiffness | Maximal mean stiffness | Maximal "responce" | |
| The minimization of the total energy
stored in a construction (or the maximization of its integral rigidity)
under some fixed loading.
Requires the search for composites which store minimal energy under
some given loading.
The problem is reduced to a non-stable variational problem of the minimization of the energy upon the structures.
|
The minimization of the total energy stored
in a construction under some uncertain or varying
loadings.
Requires the search for composites which store minimal sum of energies
under several loadings.
The problem is reduced to the minimization of the norm of somesome operator
that links the fields and the structures.
|
The minimization of other integral (weakly lower-semicontinuous) functionals,
like the norm of the displacement, displacement
in a point along a certain direction, etc.
Requires the search for composites which are simultaneously weak with
respect to a loading and strong with respect to an orthogonal loading.
The problem is reduced to minimization of the sum of the energy under a loading and the complementary energy under some other loading. |
|
|
Optimal structures: Specially oriented second-rank coated laminates or "coated ellipses" in 2D, or third-rank coated laminates or "coated ellipsoids" in 3D. The orientation of the optimal structures follows the axes of the stress tensor
The structure must be oriented along the principle axes of stress
|
Optimal structures: third-rank coated laminates in 2D, or six-rank
coated laminates in 3D. The orientation of the optimal structures may follow
the axes of the stress tensor of stay constant.
In contrast with the previous structure, it resists all loadings;
|
The whole variety of optimal structures is not described yet. The optimal structures include herring-bones,
matrix laminates, and something else... Particularly, the structures with maximally negative Poisson ratio and
the matrix lanitates with obliged branches are among the optimal
structures.
|
|
One can also obtain a composite material with an extremal effective
property when another property is bounded; for example: A material with
the maximal thermal expansion coefficient and a fixed elastic modulus.
Structural Optimization asks for a structure - layout of materials in
the composite cell - that maximizes the overall performance of an assemblage.
Optimal microstructures yield or to special range of local fields inside
them.
The optimization problem has been attacked from different directions.
For detailed discussion, see [VMSO].
Most of the approaches to the optimization problem are indirect. The
methods include:
| Establishing bounds of the range of the effective properties. The bounds do not depend on the structures, they show the limits of improvements of the effective properties (see section Bounds) |
| Modeling microstructures by special geometry, as sequential
"laminates of some rank",
"coated spheres", and by similar special geometry that allow the exact solution of the constitutive relation in a periodic cell (see section Modeling). |
|
Investigating of the fields in optimal structures. Often, the conditions of optimality allow for a clear interpretation in terms of requirements to the interior fields inside an optimal structure (see section Fields). |
| Numerical optimization of a structure, (see section Numerical modelling) |
Optimal structures are generally unstable. Indeed, they concentrate
the resistance capacities in certain directions to stay against a given
loading, therefore they are extremely sensitive to the variation of the
loadings. We are working on designs that compromise effectiveness and stability.
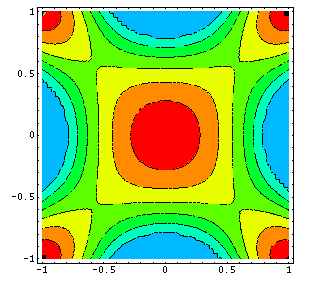 The next picture
shows the crossection of the torsioned bar with maximal rigidity. The bar
is assembled from two materials with different elastic moduli, the proportion
of the materials in the design is fixed.
The next picture
shows the crossection of the torsioned bar with maximal rigidity. The bar
is assembled from two materials with different elastic moduli, the proportion
of the materials in the design is fixed.