


Next: Expansion through limits
Up: Expansion by inversion
Previous: Creation of complex numbers
Same scheme can be applied to functions instead of numbers.
- Consider a function
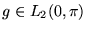
- Function
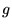 is transformed to the series of its Fourier coefficients
is transformed to the series of its Fourier coefficients 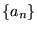
by the Fourier transform:
The sequence 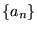 is bounded by the inequality
is bounded by the inequality
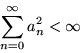 |
(1) |
for any function
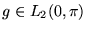 .
.
- We may complement
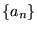 of the type (1) to the set of all
sequences, with may have unconstrained sum of the squares of their elements.
of the type (1) to the set of all
sequences, with may have unconstrained sum of the squares of their elements.
- Applying then the inverse Fourier transform we define the expansion of the
functional space
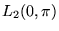 to the space of distributions
to the space of distributions ![[*]](/usr/local/share/latex2html/icons.gif/cross_ref_motif.gif) .
.
Andre Cherkaev
2001-11-16
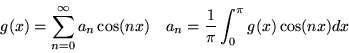
![]() is bounded by the inequality
is bounded by the inequality
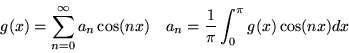
![]() is bounded by the inequality
is bounded by the inequality