

Polynomials occur ubiquitously in applications. A number of techniques have been developed for working with them and exploiting their special structure. In this class you will learn how to evaluate, factor, and divide polynomials.
Consider a polynomial such as
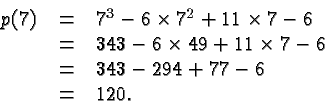
It turns out that this is a clumsy procedure.
The evaluation becomes much simpler if we rewrite ![]() as
as
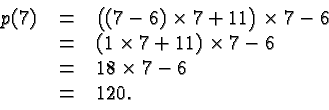
We get the same answer, of course, but the computation is simpler and
it involves fewer basic operations. The advantages of this form are
more pronounced for polynomials of high degree.
The above technique works in general and is described in the
literature as synthetic division (for reasons discussed below),
nested multiplication (for reasons that are obvious when
considering ![]() ),
or Horner's Scheme (after the English Algebraist William
George Horner, 1786-1837). It's a good rule of thumb that if
something is known under several names it is usually powerful or
otherwise important.
),
or Horner's Scheme (after the English Algebraist William
George Horner, 1786-1837). It's a good rule of thumb that if
something is known under several names it is usually powerful or
otherwise important.
You can use synthetic division to evaluate a polynomial in your head,
or using a calculator (storing just one number, the value of ![]() ).
The usual way to do it on paper is to construct a table which has the
coefficients of the polynomial in the first row, and the intermediate
results of the Calculation in the second and third rows:
).
The usual way to do it on paper is to construct a table which has the
coefficients of the polynomial in the first row, and the intermediate
results of the Calculation in the second and third rows:
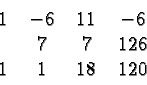
Each entry in the third row is the sum of the entries above it. In the first column there is a blank in the second row that you can think of as zero. Each entry in the second row is obtained by multiplying the entry to the lower left of it with the number at which we evaluate the polynomial (in this case 7). Usually we take note of that number by writing it to the left of the array in the first row:
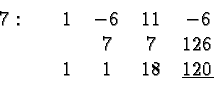
The final result of the evaluation (in this case ![]() ) is
given (and underlined) in the lower right corner of the array.
) is
given (and underlined) in the lower right corner of the array.
The process is called synthetic division because it can be
thought of as dividing our
polynomial by ![]() with remainder. The quotient is a polynomial
whose coefficients are the other entries in the last row. In
this case,
with remainder. The quotient is a polynomial
whose coefficients are the other entries in the last row. In
this case,
We write a polynomial in
standard form as a sum of monomials. In factored form a polynomial is
written as a product of lower degree polynomials. It is
completely factored if all factors are of as low a degree as
possible.
For example, you can easily check that our polynomial
The significance of having a polynomial
Factoring is emphasized in a class like this as a means of solving
polynomial equations. It works beautifully if you are able to find
the factors. However, the usual flow is often the other way, if you really
want factors you find them by first finding the roots of a polynomial.
There is, however, one special case, where you find factors that are
common to two (or more) polynomials, usually for the purpose of
canceling them in a ratio of polynomials. That subject deserves its
own page on
long division and the Euclidean Algorithm .
Factoring a Polynomial
![]() satisfies
satisfies
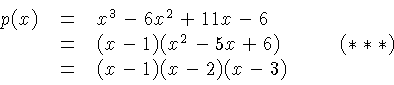
![]() in factored form
is that it makes it easier to solve equations of the form
in factored form
is that it makes it easier to solve equations of the form ![]() .
A solution of that equation is called a root
or zero of
.
A solution of that equation is called a root
or zero of ![]() .
A product is zero if and only if one of the factors is zero, so to
find the roots of
.
A product is zero if and only if one of the factors is zero, so to
find the roots of ![]() we need to look only at the roots of the
individual factors. It is clear from
we need to look only at the roots of the
individual factors. It is clear from ![]() that the roots of our
particular polynomial
that the roots of our
particular polynomial ![]() are
are ![]() ,
, ![]() , and
, and ![]() . This is not
at all obvious by looking at the original definition
. This is not
at all obvious by looking at the original definition ![]() of
of
![]() .
.