

Translating and Scaling Graphs
The applet just above this paragraph on this page can help you
understand the effects of simple shifts (or translations) and
rescalings of a graph. You can either look at the graph and deduce
the equation, or start with the
equation and figure out the graph. There is a
detailed explanation in terms of parabolas. Here we give a
summary in terms of a general function 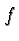 , and then explain the
operation of the applet.
, and then explain the
operation of the applet.
Suppose we start with a basic function 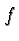 and consider its graph,
i.e.,
the graph of the equation
and consider its graph,
i.e.,
the graph of the equation
This is the basic graph and you can have the applet display it
for the following special choices of 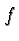 . Click on the description of
the function to see its graph. (Use the Back button of your
browser to return here.)
. Click on the description of
the function to see its graph. (Use the Back button of your
browser to return here.)
Consider now the function
for some constants 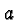 ,
, 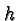 , and
, and 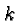 .
Naturally, the graph of
.
Naturally, the graph of 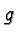 will be similar to that of
will be similar to that of
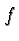 . Specifically, the graph of
. Specifically, the graph of 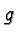 is obtained from that of
is obtained from that of
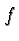 by
by
- Shifting the graph of
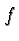
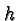 units to the right. This is
a horizontal translation of the graph.
units to the right. This is
a horizontal translation of the graph.
- Multiplying the
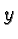 value of the shifted graph by
value of the shifted graph by 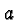 . This
is a scaling (or rescaling), of the graph.
. This
is a scaling (or rescaling), of the graph.
- Translating the shifted and scaled graph up by
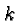 units. This is a vertical translation of the graph.
units. This is a vertical translation of the graph.
These ideas are illustrated for
in the nearby Figure.
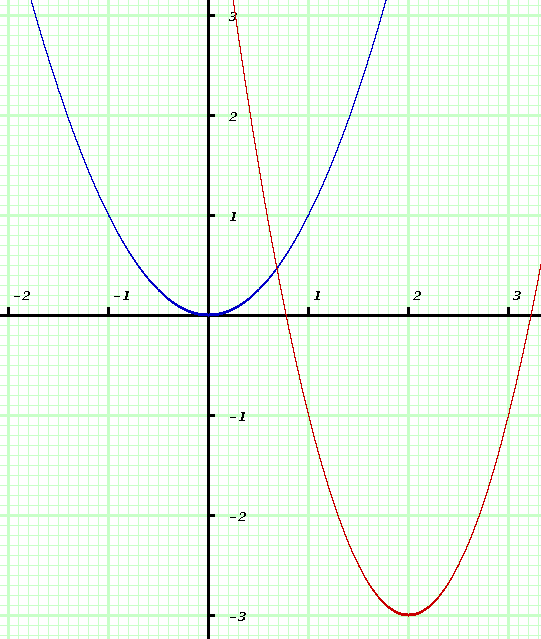
Figure 1: An Example.
The blue graph is the graph of 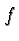 . The red graph is the graph of
. The red graph is the graph of
corresponding to 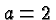 ,
, 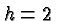 , and
, and 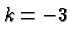 .
.
This Figure was created with the applet on this page. The remainder of
the page describes how to operate the applet.
Operating the applet.
In what follows we'll refer to the values of 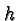 ,
, 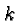 and
and 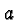 as the data and to the graph of the corresponding function
simply as the graph or the modified graph.
as the data and to the graph of the corresponding function
simply as the graph or the modified graph.
To use the software, follow these steps:
- Click on the applet on this page, where it says to click. If
your browser does not support java code then a message will appear at
the top of this page telling you so, and inviting you to view a
picture of what you want to be seeing instead of that message.
- Two windows will appear on your screen. One is a control window with
buttons to click, and places to enter data. The other shows a parabola
drawn in a coordinate system that is imposed on a fine grid resembling
Engineering graph paper. The parabola is the graph of the default
basic function
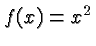 . The basic function is always drawn in
blue. The graph corresponding to the data is drawn in red. A graph
corresponding to data specified by you is drawn in magenta (purple).
. The basic function is always drawn in
blue. The graph corresponding to the data is drawn in red. A graph
corresponding to data specified by you is drawn in magenta (purple).
- You can operate the software in various modes:
- Given the data draw the graph.
- Given the graph, figure out the data.
- Specify the data and see the corresponding graph.
- The buttons on the Control Panel have the following effects:
- Quit finishes your session and causes the windows to disappear.
- New creates a new data set and corresponding graph.
- Show shows the current data and the graph.
- Erase erases the graph (in mode 1) or the data you entered
(in mode 2).
- Graph or Algebra toggles between modes 1 and 2.
- Basic toggles on and off the drawing of the basic
function. You usually want to see the basic function so you know what
you are working with, but if you wish to spice up things you can turn
the basic function off.
- Guess causes the graph of the function to be drawn that
corresponds to the current data in the text fields of the control
panel.
If no data exist, the defaults
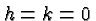 and
and 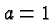 (corresponding to
the basic function) are used.
(corresponding to
the basic function) are used.
- Scale Toggles between 50 and 100 pixels per unit
length. 100 pixels look nicer, but you may have to use 50 (the
default) to show all the relevant parts of all graphs. You may be
able to resize your drawing window and use the larger scale.
- The drop down menu in the control panel lets you select a new
basic function from those described above.
- The three blue text fields show the current data, or let
you enter them. To enter a number, click on the text field, type the
number, and hit enter. If the code cannot understand what your are
typing (for example if you type the phrase "the secret value") it will
use a default value instead.
- To determine the graph do as follows:
- Select mode 1 by clicking on the button
labeled Graph if that label is present.
- Focus on the point
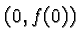 on the graph of the basic
function. For all but the last function this is the origin. For the
bell shaped function this is the point
on the graph of the basic
function. For all but the last function this is the origin. For the
bell shaped function this is the point 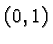 .
.
- Figure out the
corresponding point on the modified graph. Locate that point in the
drawing window and click on that point. You need to be within 12
pixels of that point.
- Find any other point on the graph more
than one unit away on the first point
and
click on it.
- If all went well the modified graph will appear and you can be
proud of yourself. If something went wrong the two points you clicked
on will disappear and you can try again. If you make a mistake and
click on the wrong point you can use the Erase button to undo your
action.
- To determine the data proceed as follows:
- Select mode 2 by clicking on the button
labeled Algebra if that label is present.
- Look at the graph in the drawing window and figure out the
data.
- Enter them in the text fields. If you enter the correct values
the corresponding text fields will change color.
- To see the graph corresponding to the data you have so far
entered click on the button labeled Guess.
- Start with a simple function, i.e.,
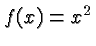 or
or
 and go on to the other functions only after you gain experience.
The last, bell shaped, function is much more challenging than the
other functions.
and go on to the other functions only after you gain experience.
The last, bell shaped, function is much more challenging than the
other functions.
- When all three text windows have changed color you have
succeeded and you can again feel proud.
- To see various graphs select mode 1 and click repeatedly on
New. To see the data corresponding to a particular function click on
Show.


![]() , and then explain the
operation of the applet.
, and then explain the
operation of the applet.
![]() and consider its graph,
i.e.,
the graph of the equation
and consider its graph,
i.e.,
the graph of the equation

![]() . The red graph is the graph of
. The red graph is the graph of
![]() ,
, ![]() and
and ![]() as the data and to the graph of the corresponding function
simply as the graph or the modified graph.
as the data and to the graph of the corresponding function
simply as the graph or the modified graph.