

A rational expression is an algebraic expression that can be written as the ratio of two polynomial expressions. A rational function is a function whose value is given by a rational expression. Examples for rational functions (and associated expressions) include:
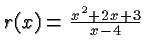 . This expression is obviously
the ratio of two polynomials.
. This expression is obviously
the ratio of two polynomials.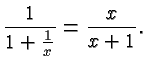
Examples of algebraic expressions that are not rational can be constructed similarly as in the case of polynomials .
Another useful way of thinking about polynomial and rational expressions is that polynomial expressions are those algebraic expressions that can be evaluated using a finite number of additions and multiplications (and subtractions), whereas rational expressions may also require division for their evaluation. However, no operations beyond the basic four arithmetic operations are required to evaluate a polynomial or a rational expression.
We must not divide by zero, and hence a rational expression is undefined if the denominator is zero. For example, the rational expression
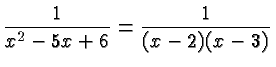
There is just one fundamental principle governing the manipulation of rational expressions, and that is that they work exactly like fractions . Indeed, that is the main reason why fractions should still be emphasized in the elementary and secondary school curriculum. You may encounter the view that fractions are obsolete because calculators are ubiquitously available and it's more convenient to work with decimal numbers. However, not understanding fractions makes it impossible to understand algebra.
Understanding fractions, and appreciating the fact that rational
expressions are like fractions is all you need to know to handle
rational expressions successfully. However, for reference the
remainder of this page lists the rules of fractional and rational
algebra, and illustrates them with an example. So suppose that
![]() and
and
![]() are rational expressions where
are rational expressions where
![]() ,
, ![]() ,
, ![]() and
and ![]() are polynomial expressions. (This
includes the special case that the polynomials are constants and the
rational expressions are fractions.)
are polynomial expressions. (This
includes the special case that the polynomials are constants and the
rational expressions are fractions.)
Then the following rules hold:

It is worthwhile to think for a moment about why these rules are true.
If the polynomial expressions are evaluated at specific values of the
variable they turn into numbers and the rules turn into
statements about fractions which hold as discussed on the
fraction page .
This is true for all possible values of the
polynomials, and that's just what we mean by the equations in ![]() .
We always reduce our problem to
one that we have solved before .
.
We always reduce our problem to
one that we have solved before .
Let's illustrate the rules with some very simple examples. Make sure you understand them! Suppose
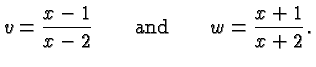
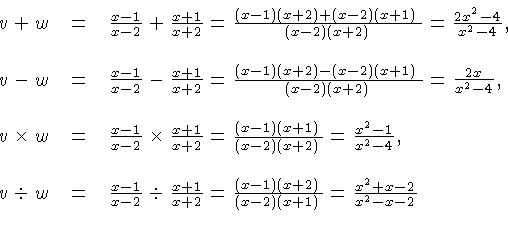
In all of these cases, the final expression are in lowest terms, i.e., there are no factors that can be canceled in numerator and denominator.
The only possible pitfall is that we must avoid division by zero. That's easy to do when dealing with specific numbers but it's sometimes subtle when dealing with variables.