

An equation is linear if it can be written in the form
Let's first ask what kind of solutions are possible for a linear
equation. There are three cases:
Suppose
No Solutions
Suppose
Suppose
Clearly there are no other possibilities, and we note the important
fact that a linear equation may have none, one, or infinitely many
solutions. It is not possible, for example, that a linear equation
has two solutions.
The crux of solving a linear equation is to recognize that the
equation is linear, and to convert it to the above simple form.
In the remainder of this page this process will be illustrated for
increasingly complex equations.
The material on this page illustrates three of our
principles:
Applying the same operation on both sides of a
valid equation gives another valid equation.
Below you will see several examples of how an equation whose linearity
is not obvious can be converted to a clearly linear equation. The
examples cover most or all of the techniques required for this class,
but of course the list is nowhere near being exhaustive.
We subtract
We subtract
We apply the distributive law on both sides and obtain
The two sides are the same if their reciprocals are the same, and so
obtain an equation like that
in Example 1:
Replacing the two sides with their reciprocal does not help in this
case. We need to get rid of the denominators. To that end we multiply
with both denominators on both sides and obtain
Those are the principles, in a nutshell. There are of course a great
many more examples and exercises in your textbook.
It is important to realize that not all equations are linear.
For example, the equation
A Unique Solution
![]() . In that case there is one and only one solution,
namely
. In that case there is one and only one solution,
namely
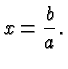
![]() has the
solution
has the
solution ![]() , and there is no other solution. We say that the
equation has a unique solution. This is by far the most frequent and
the most important case.
, and there is no other solution. We say that the
equation has a unique solution. This is by far the most frequent and
the most important case.
![]() and
and ![]() . In this situation we have an
equation like
. In this situation we have an
equation like ![]() and clearly there is no solution.
and clearly there is no solution.
Infinitely Many Solutions
![]() and
and ![]() . In this situation we have the
equation
. In this situation we have the
equation
![]() and this is clearly true for all values of
and this is clearly true for all values of ![]() . There are
infinitely many solutions.
. There are
infinitely many solutions.
![]()
![]() and
and ![]() on both sides and obtain the new and
equivalent linear equation
on both sides and obtain the new and
equivalent linear equation
![]()
![]()
![]() on both sides and obtain an equation similar to
that in the preceding Example.
on both sides and obtain an equation similar to
that in the preceding Example.
![]()
![]()
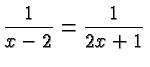
![]()
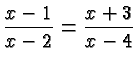
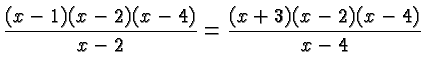
![]()
Nonlinear Equations
![]()
![]() and
and ![]() , and it is not linear.
Since it has two solutions, which is not possible for a linear
equation, we can tell without trying that it cannot be converted into
, and it is not linear.
Since it has two solutions, which is not possible for a linear
equation, we can tell without trying that it cannot be converted into ![]() .
.