Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

Solving Inequalities

An inequality consists of two algebraic expressions connected by one of the symbols $ < $, $ \leq $, $ \geq $, or $ > $. These symbols are explained on the page discussing the real number line. There might also be the symbol $ \neq $, but the other cases occur more frequently.

Suppose we have an inequality involving some variable $ x $. (It might be called something else, however.) To solve the inequality (for $ x $) means to convert it to an equivalent inequality of the form

$\displaystyle x \bullet R $

where $ \bullet $ is one of the above symbols and $ R $ is an algebraic or arithmetic expression (often just a plain number) that does not contain $ x $.

For example, suppose we know that

$\displaystyle x-3 < 7. $

Clearly this is true if and only if

$\displaystyle x < 10 $

which is an inequality of the desired form.

Formally speaking we converted the initial inequality by adding 3 on both sides. Why can we do this, and what else can we do?

Two fruitful ways of thinking about inequalities are in terms of the real number line, or in terms of an old fashioned scale. Having an inequality means that one side of the scale is heavier than the other. Adding the same weight on both sides of the scale, or multiplying with a positive factor (e.g., doubling) on both sides leaves the heavier side heavier. (One can contemplate more involved operations, for example adding more on the heavier side than on the lighter side, which also leaves the heavier side heavier. But we will only use the most basic techniques in this class.) In terms of the real number line, if we have an inequality then one point is to the left of the other, and shifting both points to the left or right by the same amount does not alter the relationship.

There is one subtlety, however. Multiplying on both sides with the same negative factor reverses the relationship. Suppose for simplicity that we multiply with $ -1 $. In terms of the real number line we reflect a point through the origin. In terms of the scale, a weight that previously pushed downwards now pulls upwards. If we have two points, rotating around the origin flips the points, the one that previously was to the right of the other is now to the left.

Here is a simple example. We know that

$\displaystyle -5 < 1. $

If we multiply with $ -1 $ on both sides we get the numbers $ 5 $ and $ -1 $, but

$\displaystyle 5 > -1. $

The multiplication with the negative factor reversed the sign!

So basically we process inequalities the same way as we process equalities, except that we take care to reverse the sign when we multiply on both sides with the same negative factor. There are some things (such as squaring) that we can do easily with equalities, but where we have to be careful with inequalities.

For the purpose of this class we will only consider the operations of adding and subtracting the same term on both sides, multiplying with the same positive factor on both sides, and multiplying with the same negative factor on both sides. The first two operations leave the inequality unchanged, the third reverses the sign.

Let's see these principle in action in some examples:

Checking your answers.

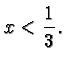
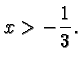
To check your answer replace the inequality with an equality and see that the original equality (formerly an inequality) is satisfied. Also ask yourself what happens if you increase the variable and see if the answer to that question is consistent with your result. In the last example above, when $ x=3 $ we have that $ 3x+4 = 13 = 5x -2 $ which is consistent with our result. Moreover, when we increase $ x $ we increase the right side of the original inequality more than the left (because of the factor 5 on the right being larger than factor 3 on the left) and so the left side grows more slowly than the right, which is also consistent with our result.