The concept of a function is more central in mathematics than the concept of a number. In this class we use functions only in a very narrow context, but if you go on in mathematics you will encounter functions ubiquitously in every class you take.
For the purposes of this class, you can think of a function as a
machine that takes a number (the input), processes it, and produces
another number (the output). A given input always produces the same
output, but the same output can be produced by different inputs. The
way a particular function processes the input is usually described by
an algebraic expression (sometimes called the rule). Processing a particular input
![]() is
called evaluating the function at
is
called evaluating the function at ![]() .
The set of all numbers for which you can in fact evaluate the function
is called the domain of the function,
the set of all possible outputs you obtain in this manner is called
the range of the function.
.
The set of all numbers for which you can in fact evaluate the function
is called the domain of the function,
the set of all possible outputs you obtain in this manner is called
the range of the function.
For example, consider the equation
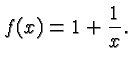
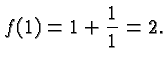
Sometimes you will be asked to determine the domain of a function. There are more subtle situations, but in this class the domain is always the set of all real numbers, except those where you cannot evaluate the expression. Usually the only reason you might be unable to evaluate a function is that the relevant expression might call for a division by zero, or the computation of a square root of a negative number.
For example, the domain of the function
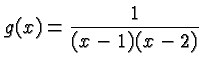
It is easy to be confused about just what it means to evaluate a
function. Functions can be evaluated not just at numbers, but also at
algebraic expressions, and at other function values. Let's look at
some examples. Suppose that ![]() is defined
is defined
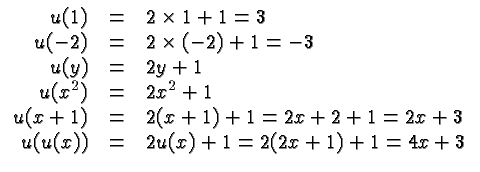
Functions can be combined in various ways to create new
functions. Suppose ![]() and
and ![]() are two functions, and
are two functions, and
![]() is one of the arithmetic operations
is one of the arithmetic operations ![]() ,
, ![]() ,
,
![]() , or
, or ![]() . Then a new function
. Then a new function
For example, suppose as before that
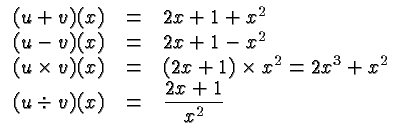
A function can be evaluated at the value of another (or the same)
function. This is called the composition of functions. The
composition ![]() of two functions
of two functions ![]() and
and ![]() is denoted by
is denoted by
Note that, on the other hand,
Thus
There are subtle issues regarding the domain and range of the
functions involved. In particular, when we consider a composition
like
The graph of a function
![]() the range of
the range of ![]() must be a subset of the domain of
must be a subset of the domain of
![]() .
.
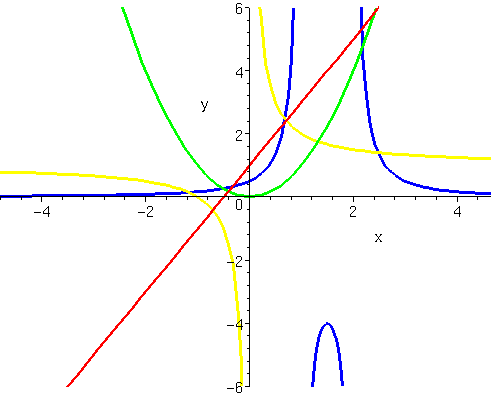
Graph of a function.
![]() is the
graph of the equation
is the
graph of the equation
![]()
![]() (yellow),
(yellow), ![]() (blue),
(blue), ![]() (red), and
(red), and ![]() (green).
(green).