How to Figure Things Out
This page describes some proven ways in which you can be more
efficient and effective when actually doing mathematics with paper and
pencil. It focuses on
how to do what you do. (Almost all the of other pages in this
course focus on what to do.)
Students often think that the
only purpose of figuring things out is to get the answer with the
minimum amount of fuss and effort, and to get it over with. Actually
there are several objectives:
- First and foremost, you want to get the right answer. Mistakes
are easy to make, and they occur with dismaying frequency. In many
cases they are not immediately obvious and they invalidate everything
that follows. As a result people waste huge amounts of time.
- You want to be able to go back while you are figuring and see
what you did, and what went wrong, if you did make a mistake.
- You want to recognize any mistakes as soon as possible so that
you don't waste your time on meaningless calculations.
- If your work is going to be read (and perhaps evaluated) by
someone else you want that person to understand what you did.
- In a math class (like most certainly in this one) everything you
do builds on what you did before and so you want to be able to go back
to what you did some time ago--even if you already turned in the
answers and got credit for them--and understand what you did back
then. In the same vain, you want to understand and
remember what you did
because you are bound to need it in a future problem.
- You want to learn what there is to learn from the particular
piece of figuring that you are doing.
- Subject to accomplishing the above objectives you want to spend
as little time as possible on any particular problem.
Luckily, the last objective is perfectly consistent with the others if
you think in terms of the whole set of problems and exercises that you
do in the course of the semester. If you guard carefully against
errors and ensure that you can correct them easily soon after they
occur you save time. If you learn what there is to learn in each
problem then you have to do fewer problems and exercises overall, and
you are able to do future exercises more quickly and with less
frustration.
Of course, how to figure things out is a highly personal process, and
what works for you may not work for somebody else, and vice versa.
However, I wrote this page because over and over I see students approach problems in a way that does not work at all, for them, or anybody else.
So here are some suggestions:
- Before you start a problem think about your expectations. If a
contradiction to those expectations arises as you work the problem
pause and figure out what happened.
- Students usually seem to be in a rush when trying to solve a
problem. That's understandable, there is much to do and little time.
But actually it is much more efficient, and
faster, to go about solving a problem carefully and
deliberately, taking small steps, writing down each step, and
making sure each step is correct before going on. Doing so reduces
the number of errors, makes you more alert to errors when they do
occur, and reduces the time you spend on identifying and correcting
errors.
- When algebraic expressions are equal write an equality sign
between them. Write the expressions in the sequence in which they
occur. Don't just scribble them unconnected all over the page
wherever there is some as yet unused space.
- Use engineering type graph paper instead of blank or lined paper.
This is particularly useful when drawing graphs. Don't use "scrap"
paper with unrelated information on one side. It will only confuse you
and your reader.
-
Use a soft pencil and an eraser. Don't use a pen, since scribbeling
out errors and perhaps writing over them makes your writing
incomprehensible. Don't use a hard pencil that writes only faintly,
it's hard to read.
- When writing a sequence of equations or steps line them up so the
logical connection is clearly apparent.
- When you change an expression or equation don't modify what you
wrote. Don't erase or cross out things (unless they were
wrong). Instead write the entire new expression or equation.
(Sometimes it makes sense to cross out terms that cancel. In that
case do so, but make sure it remains clear what actually did cancel.)
- Take a note of what you did in each step, don't just do it, and
then later wonder why you could take that step.
- Continue to ask yourself whether what you have currently makes sense.
- Think about the physical meaning of what you are doing. This is
one of the major reasons to use variables rather than numbers. You
can't add a distance to a weight, for example, and so if your figuring calls for that
then you know that
something has gone wrong. You can recognize this in the expression
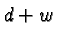but not in the expression 
.
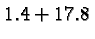- Keep your writing neat and organized.
- Label your axes and note what your variables mean.
- Remember that upper and lower case letters are different in
mathematics.
- Use meaningful names for your variables (e.g.,
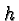for
height,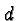 
for distance, 
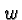for weight, 
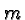for mass, etc.).
- Always check your answers. If you solved an equation
substitute your answers in the original equation. Compute the same
answer in two different ways. If your answer is a formula see that it
gives the right particular value in a case where you know the
answer. Check identities (equations that are true for all values of
the variables) by substituting particular values. Draw a picture and
see that your algebra is consistent with the picture. Ask if your
answers meet your expectations. Do they make sense?
- When you are done take a moment to reflect on what you learned.
Chances are you will need to use this new knowledge in a
subsequent problem, and thinking about it now will make it easier to
recognize when you need it in the future.
- Keep your notes, including all your worked exercises, organized
for future reference.
- A major mathematical problem solving technique is to simplify a
difficult problem, solve the simple problem, and apply what you
learned in the process to the difficult problem. In the context of a
class like this, if you are stuck on a problem, chances are that you
already solved a simpler problem that's relevant to your current
problem. So if you are stuck, look back over problems you solved
recently to see if something you did there applies to what you are
doing now.
- Don't spin your wheels. If you still can't solve a problem go back
over your notes, read in your documentation (these web pages or your
textbook), talk with friends, tutors, or your instructor, or set aside
the problem and solve some others before returning to the
obstacle.
You'll find examples for many of these techniques throughout these web pages
and the solutions of the homework problems.