

The principles illustrated for parabolas apply to other graphs as well. We illustrate them here for circles (which are a special case of ellipses) and hyperbolas.
Consider the circle of radius ![]() around the origin. This particular circle is sometime called
the unit circle. It is the set
of all points
around the origin. This particular circle is sometime called
the unit circle. It is the set
of all points ![]() whose distance from the origin is
whose distance from the origin is ![]() 1. By the
Pythagorean Theorem the unit circle is the graph of the equation
1. By the
Pythagorean Theorem the unit circle is the graph of the equation
Consider again the special case that the center of a circle is the
origin and its radius is
![]() .
Then its equation can be rewritten as
.
Then its equation can be rewritten as
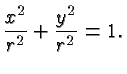
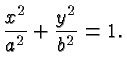
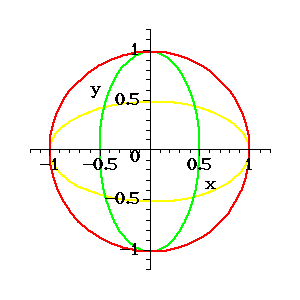
Figure 1. Circles and Ellipses
Figure 1 shows the unit circle in red, the ellipse with
![]() in yellow, and the ellipse with
in yellow, and the ellipse with
![]() in green.
in green.
An ellipse can be translated so that its center is at
![]() ) which gives rise to the equation
) which gives rise to the equation
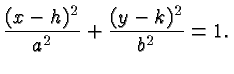
Note how all the relevant information about the ellipse, i.e., its center and the lengths and orientations of its major and minor axis, can be read directly from this equation.