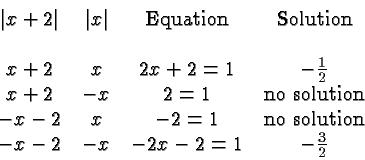Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

Solving Equations Involving Absolute Values

The absolute value of a number $ x $ is its distance from the origin. For every (non-zero) distance there are two numbers with that distance from the origin, a positive and a negative one. That is the only fact peculiar to absolute value equations that you need to understand and appreciate. All absolute value equations in this class can be approached using this simple principle.

For example, if we know that

$\displaystyle \vert x\vert = 3 $

then either $ x=3 $ or $ x=-3 $.

Let's consider more examples. Suppose

$\displaystyle \vert x+2\vert = \vert 2x -1\vert $

There are two possibilities for the left hand side of this equation:

$\displaystyle \vert x+2\vert = x+2 \qquad\hbox{or}\qquad \vert x+2\vert = -(x+2) = -x -2. $

Similarly there are two possibilities for the right hand side of the equation:

$\displaystyle \vert 2x-1\vert = 2x -1 \qquad\hbox{or}\qquad \vert 2x-1\vert = -(2x-1) = -2x + 1. $

We can now combine the various cases and obtain four equations:

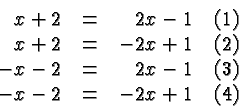
\begin{displaymath} \begin{array}{rcrr} x+2 &=& 2x-1 & (1) \\ x+2 &=& -2x+1 ... ...2 &=& 2x-1 & (3) \\ -x-2 &=& -2x+1 & (4) \\ \end{array} \end{displaymath}

Of these the fourth equation can be obtained from the first, and the third from the second, by multiplying with $ -1 $ on both sides of the equation. Therefore we need to consider only the first two equations. The first equation has the solution $ x=3 $ and the second $ x=-\frac{1}{3} $. It's easy to check (and you should do so) that both solutions satisfy the original equation.

The above example is typical: we look at all possible sign combinations of the expressions of which we take absolute values, and prune the set by looking for equivalent equations.

Sometimes there are subtleties. Here is another example: Suppose

$\displaystyle \vert x+1\vert =\vert x+2\vert $

Considering different cases we again obtain two equations

$\displaystyle x+1 = x+2 $

and

$\displaystyle x+1 = -(x+2) = -x-2. $

The last equation has the solution $ x=-\frac{3}{2} $, which is also a solution of the original equation. However, there is no number $ x $ such that $ x+1= x+2 $. The original equation, therefore has only one solution!

So we solve an absolute value equation by replacing it with several equations that do not involve absolute values, and solving each one of them. Sometime the replacement equations have solutions that are not satisfied by the original equation. A simple example is given by

$\displaystyle \vert x\vert = -1 $

which leads to the replacement equations $ x=-1 $ and $ -x=-1 $. However, neither $ x=1 $ nor $ x=-1 $ solve the original equations.

Of course in this example it is obvious that there is no solution since the absolute value of anything is never negative. Another less obvious example is given by

$\displaystyle \vert x+2\vert + \vert x\vert = 1. $

The following table illustrates all possibilities

\begin{displaymath} \begin{array}{cccc} \vert x+2\vert & \vert x\vert & \hbox{Eq... ...on} \\ -x-2 & -x & -2x-2 = 1 & -\frac{3}{2} \\ \end{array} \end{displaymath}

Two of the four equations have no solutions. Moreover, it's easy to check (do it) that $ x=-\frac{1}{2} $ and $ x=-\frac{3}{2} $ do not satisfy the original equation. Indeed, that equation has no solution.