 |
In this section, a simple but nontrivial example of use of IBIS
is given. The example shows the power of the immersed boundary method,
and the simplicity
of using IBIS. The example is artificially contrived, but an experiment
identical to the example could be conducted the results checked.
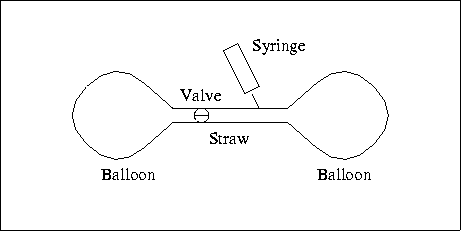
For the actual experiment, the following equipment is needed: a pale of water, two equally sized balloons, a valve, a straw, and a syringe. To construct the experimental apparatus, attach the balloons to the two ends of the straw and insert the valve and syringe into the straw. The basic setup would then appear as shown in Figure 1.
To set the initial state of the apparatus, the valve is opened, and the system is injected with enough water so that each balloon is slightly stretched. Then the valve is closed and additional water is added to the system so that one balloon contains more water than the other and therefore, is stretched more. The apparatus is placed in the pale of water and all the fluid is allowed to settle. Once the fluid has settled the experiment begins by opening the valve. The experiment ends when the fluid settles again.
The expected outcome of the experiment is easy to guess. Since one balloon is stretched more than the other, it has more stored energy. This energy differential will drive fluid from the larger balloon to the smaller balloon until the stored energies of the two balloons are equalized. If the two balloons have identical elastic properties, they will be of equal size and shape at the end of the experiment. Furthermore, since no fluid enters or leave the balloons and straw during the experiment, the volume of the fluid in the apparatus is conserved.
While this is a simple experiment with little doubt about what the outcome will be, this is a nontrivial computational exercise unless the immersed boundary method is employed. The only other method for solving this problem known to the authors would be to employ a finite element method. While a finite element solution of the problem would be straightforward, the computation would be difficult to implement because of the moving boundary, and expensive to compute because of the lack of a regular grid and because the grid would change in time.
To setup this apparatus as a computational experiment using IBIS, two steps are required. First, it is necessary to estimate the elastic properties of the balloons and the physical parameters of the fluid such as viscosity and density. The fluid parameters are available from several sources, notably the CRC Handbook of Chemistry and Physics.
The elastic properties utilized by IBIS are modeled by an elastic link system. The parameters of this system have not been measured for real objects, and so they are not documented in the literature. Thus some educated guesses need to be made. To assist with this process, Section 7 gives a dimensional analysis of the parameters and gives general guidelines for choosing them.
The next step in initializing an IBIS simulation is the specification of the initial positions of the immersed boundaries. This is accomplished by writing a program in a programming language created specifically for IBIS. A sample program for the balloons and straw experiment is contained in the following IBIS code. This code is part of the IBIS package and is named IBIS/ibisfiles/balloon.ibis
domain 0.00 4.00 0.00 2.00 grid 7 0.40e-04 10000 fluid -m 1.6 -r 1.0 -u 0.0 # # visualization parameters # visual -h 256 -w 512 -n 100 -p binary -b balloon graph -n 500 -p line -b balloon -d 1 particle -d 4 # # reset default spring parameters # spring b -b 1.0e+6 -s 4.0e+7 spring r -b 1.0e+6 -s 4.0e+7 -t 4.0e+6 # # apparatus # polygon first 1.50 0.875 ray 2.50 0.875 -n 256 bcurv s 6 -n 512 -e 4.0e+6 2.50 0.50 3.00 0.25 3.50 1.00 3.00 1.75 2.50 1.50 2.50 1.125 ray 1.50 1.125 -n 256 bcurv s 6 -n 512 -e 4.0e+6 1.50 2.00 0.50 2.50 -0.50 1.00 0.50 -0.50 1.50 0.00 1.50 0.875 end
This code has three basic sections. The first section, consisting of the top five line, specifies the physical, computational and graphical parameters for the IB calculation. The first two lines specify the physical and computation domain, the third line specifies the fluid variables, the fourth and fifth lines specify visualization variables.
The second section of the code, consisting of the fifth and sixth lines, specifies the elastic link attributes of the apparatus. The elastic link parameters for this calculation were chosen so that the straw is nearly inelastic, and the balloon have identical elastic properties and are easily deformed.
The third section, beginning at the line labeled ``polygon'' specifies the positions of the initial immersed boundaries. The balloons and straw apparatus is constructed as a piecewise curve. By plotting the data pairs on the lines after polygon and connecting the dots, the basic shape of the apparatus can be seen.
Once this file is created, it is run through the IBIS preprocessor which interpretes the IBIS program, creates input for the IB model solution programs, and displays the initial conditions for the simulation as shown in Figure 2.
To execute the preprocessor, execute the following commands from the IBIS directory
>> ibisdir balloon
>> cp balloon.ibis balloon
>> cd balloon
>> preibis balloon.ibis
The preprocessor will create the model solution programs and set up
the subdirectories needed to store the output.
At this point, the balloon subdirectory contains six files. These files and their contents are;
Fcode <- FORTRAN numerical software
README <- Directory log file
balloon.ibis <- The IBIS source file
binary <- The subdirectory for color graphics
ibisdat <- Data created by and for IBIS
line <- The subdirectory for line graphics
The IBIS model solution programs are then used to solve model equations for the interactions between the fluid and elastic apparatus. To execute the IB solver, execute the following command
>> ibis
During the solutions of the model equations, several forms of graphical
output are produced. One set of output is presented in Figure 3. There
a sequence of snapshots of the solution are presented at several times.
The snapshots computationally confirm the expectations of the outcome of
the experiment, namely size and shape of the large balloons and small balloon
equalize. These snapshots were created with IBIS software and format
conversion programs that are freely available on the internet. There will
be 101 files of this type created by the simulation because the simulation
takes 5000 time steps and produces a graph every 50 time steps.
To view any of color graphics files, during or after the numerical calculation, type
>> show n
where n is a file number ranging over the integers from to 100.
If the program responds that the file does not exist, then you have attempted
to see a file before it was calculated, so either decrease n or wait
for a while.
Once about 20 files have been created, an animation of the solution can be seen. To initialize and run the animation, type
>> play
The last two programs, play and show are not quite as simple as they appear,
but almost. These programs are specifically designed to be front ends for
two other programs that actually display the data and create the animation.
Play and show are provided for convenience.
The other type of graphics output files are line type plots. These files are considerably more data intensive and require more computational power to produce. Therefore, the user will typically produce fewer of these graphs. However, the tradeoff in size is made up in the quality and type of information these files produce. An example of these graphs is shown in Figure 3. This graph shows a time snapshot of the simulation but with more detail about the fluid dynamics. In particular, the line plot produces velocity vectors that can be scaled to show more detailed information about the fluid motion. These line plots provide more quantitative information about the simulation, while the color graphics just desribed provide a better qualitative picture of the dynamics of the simulation.
The core software that produces the line graphs is significantly harder to use than the software that produces the color graphs. Therefore, the IBIS graphics package also provides a graphical user interface to simplify the graphical exploration of the computed data. This program is called ibisview. ibisview can be used to see both the color and line graphics, to execute the animations, and to zoom into graphics files in color, line or animated forms. It should be used in favor of the core software.
Figure 4 shows the graphical user interface created by ibisview. The image shows the line graphics data plotted at the 500th time step. ibisview gives the user considerable flexiblity in viewing the ibis data, for example, the the user can step through the data files, zoom onto a region of the simulation, save the graphs in various formats, create mpeg movies, and produce hard copy output among other features.
The command buttons in ibisview allow the user to examine individual color plots and create animations, to examine individual line plots and, using the mouse, to create zoom plots of the IB data, and to save the data in a number of different formats. These formats include pixel maps suitable for inclusion in other computer applications, and line plots suitable for inclusion in papers and reports. It is also easy to control which elements are being plotted on the line plots, for example on could create a graph with the links between immersed boundary points, but not plot the immersed boundary points themselves.
The IBIS implementation of the immersed boundary method should allow a novice user to perform this calculation from scratch within a few hours of first seeing and reading this document. The IBIS program can be easily interpreted and new programs easily written.
The balloon.ibis example will be used throughout this document as the primary example for the use of the code. More involved experiments will also be presented where they are appropriate in this manual. In particular, the IBIS code has the ability to actively control the immersed boundaries, and the balloons and straw example will be used to show these abilties by periodically squeezing one of the balloon. This example will be given in section 5. IBIS also allows for the specification of sources and sinks of fluid. This too will be demonstrated in section 5.