Kurt Vinhage
Email: vinhage@math.utah.edu
Office: JWB309
Welcome to Kurt Vinhage's website! Here you will find important information regarding teaching, current research activities, and a (reasonably) updated CV/Resume. Feel free to look around!
Teaching
Research Interests
Smooth Dynamical Systems, Algebraic and Homogeneous actions, Higher-rank actions, Rigidity and Flexibility, Measurable Invariants of Smooth Systems
Papers
- On the Rigidity of Weyl Chamber Flows and Schur Multipliers as Topological Groups, Journal of Modern Dynamics, Volume 9
- Cocycle rigidity of partially hyperbolic abelian actions with almost rank one factors, Ergodic Theory and Dynamical Systems
- Local Rigidity of Higher Rank Homogeneous Abelian Actions: a Complete Solution via the Geometric Method (Joint with Zhenqi Jenny Wang), Geometriae Dedicata
- On the non-equivalence of the Bernoulli and K properties in dimension four (Joint with Adam Kanigowski and Federico Rodriguez-Hertz), Journal of Modern Dynamics
- Slow Entropy of Some Parabolic Flows (Joint with Adam Kanigowski and Daren Wei), Communications in Mathematical Physics
- Kakutani Equivalence of Unipotent Flows (Joint with Adam Kanigowski and Daren Wei), Duke Mathematical Journal
- Cartan Actions of Higher Rank Abelian Groups and their Classification (Joint with Ralf Spatzier), Journal of the American Mathematical Society
- Entropy rigidity for 3D conservative Anosov flows and dispersing billiards (Joint with J. De Simoi, M. Leguil and Y. Yang), Geometric and Functional Analysis
- Slow entropy of higher rank abelian unipotent actions (Joint with A. Kanigowski, P. Kunde, and D. Wei), Journal of Modern Dynamics.
- Instability for rank one factors of product actions, Preprint.
- Anosov actions: classification and the Zimmer Program (Joint with D. Damjanovic, R. Spatzier and D. Xu), Preprint.
Resource Archive
Pre-REU 2023
pre-REU 2024
Brin Summer School 2023 Notes
Fun Math Websites
Below, find the smooth time change of a linear flow. In the first GIF, the red points move with the linear flow, and the green and blue correspond to slow-downs of varying degeneracies. Notice that the orbits eventually re-align! In the second, you can see this slowdown affects a box in linear flow on a torus.
Slowdown of vertical flow
|
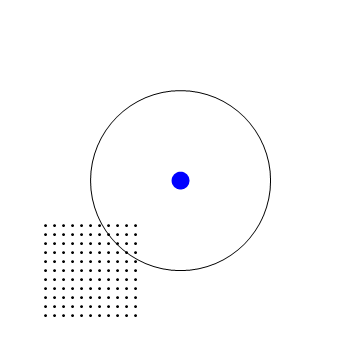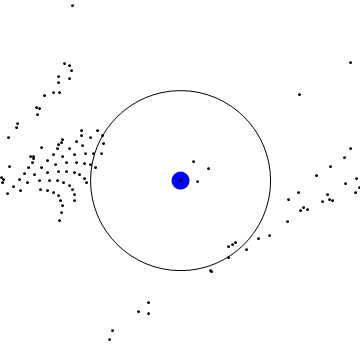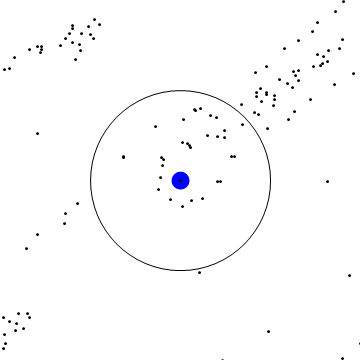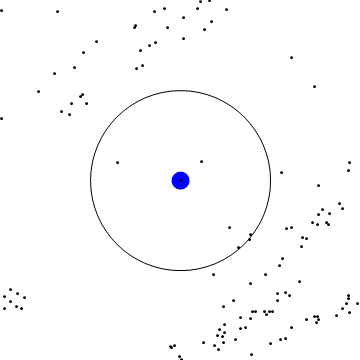
Slowdown of flow on 2-torus
|
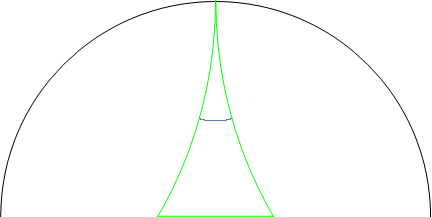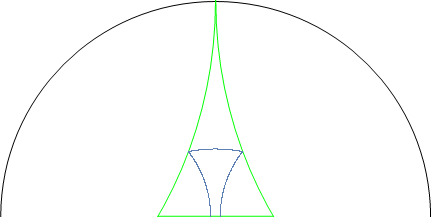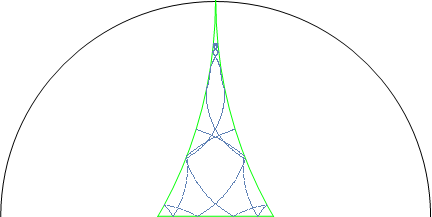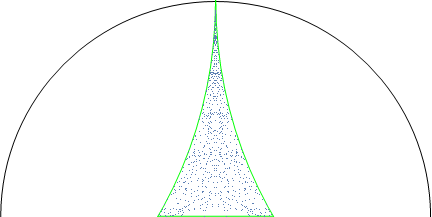
Below find a fundamental domain of the modular surface, and periodic horocycles on it sampled at 4000 points. In the first animation, they move ``downward'' in the Poincare disc model by applying the geodesic flow, eventually equidistributing. In the second figure, the half space model is used (rotated from standard conventions), and you can see the points distributing the the hyperbolic volume (more dense closer to the bottom).
