RESEARCH

Research interests

Postdocs

Graduate students

APMA receptor trafficking and synaptic plasticity

In many regions of the brain, neurons are found to exhibit bidirectional plasticity in which the strength of a synapse can increase or decrease depending on the stimulus protocol. Long term potentiation (LTP) is a persistent increase in synaptic efficacy produced by high-frequency stimulation of presynaptic afferents or by the pairing of low frequency presynaptic stimulation with robust postsynaptic depolarization. Long-term synaptic depression (LTD) is a long-lasting decrease in synaptic strength induced by low-frequency stimulation of presynaptic afferents. There is growing experimental evidence that a major component of the postsynaptic expression of LTP and LTD is the regulation of AMPAR trafficking, which results in changes in receptor number at the postsynaptic membrane, and hence modifications in synaptic strength. The total number of synaptic AMPARs is determined by a nonequilibrium steady-state, in which the flux of receptors between the synaptic and extrasynaptic regions of the postsynaptic membrane is balanced by the rate of exchange of receptors with intracellular recycling pools. We have recently developed a model of AMPA receptor trafficking between multiple dendritic spines distributed along the surface of a dendrite. Receptors undergo lateral diffusion within the dendritic membrane, with each spine acting as a spatially-localized trap where receptors can bind to scaffolding proteins or be internalized through endocytosis. Exocytosis of receptors occurs either at the soma or at sites local to dendritic spines via constitutive recycling from intracellular pools. These various processes are represented in terms of a reaction-diffusion equation. Solutions of this equation allow us to calculate the distribution of synaptic receptor numbers across the population of spines, and hence determine how lateral diffusion contributes to the strength of a synapse. We are currently using our model to investigate the role of AMPAR trafficking in various forms of synaptic plasticity and in neurodegeneration associated with a number of diseases such as Alzheimer's.

Relevant publications

Stochastic models of motor-assisted transport in dendrites

Although most proteins destined for dendrites and dendritic spines are conveyed from the cell body, a subset of mRNAs are transported into dendrites to support local protein synthesis. Increasing evidence indicates that local protein synthesis in dendrites plays a critical role in mediating the enduring changes in synaptic structure and function that underlie long-term memory. Within dendrites mRNA is assembled into granules, which then undergo rapid bidirectional transport via molecular motors such as kinesin. The rapid transport is interspersed with periods of slow movement or pauses, consistent with localization at synaptic sites. We are currently developing a stochastic model of mRNA transport along dendrites, which extends a previous model of NMDA receptor transport during synaptogenesis. In the latter case, the sites of slow movement appear to be associated with exo/endocytoic zones where there is cycling of receptors between the plasma membrane and the cytoplasm. Such cycling could provide a mechanism for delivering the receptors to the dendritic surface, thus making them available for recruitment to emerging synapses. For simplicity, we take synaptic sites to be distributed along a one-dimensional dendritic cable. Within each site granules undergo transitions between a mobile and an immobile state. Whenever a granule exits a site, it undergoes motor-assisted transport to the next site of exo/endocytosis along the cable. Solutions of the model equations determine the time--dependent distribution of granules along the dendrite. Coupling the transport model with synaptic signaling cascades provides a framework for studying the role of local protein synthesis in long-term plasticity.

Relevant publications

Recurrent network models of primary visual cortex (V1)

The responses of neurons in sensory cortices are affected by the spatial context within which stimuli are embedded. In primary visual cortex (V1), orientation-selective responses to stimuli in the receptive field (RF) center are suppressed by similarly oriented stimuli in the RF surround. Suppression from the RF surround, which may represent the neural correlate of perceptual figure-ground segregation, is traditionally thought to be generated within V1 via horizontal connections. Recently, it has been shown that these connections are too short and slow to mediate fast suppression from distant regions of the RF surround. In collaboration with Alessandra Angeluci (Moran Eye Center), we have developed a recurrent network model of V1 in order to show how feedback connections, which are faster and longer range than horizontal connections, can generate far surround suppression. Our model provides a solution to how suppression can arise from excitatory feedback contacting predominantly excitatory neurons. It also makes the novel prediction that the "suppressive far surround" is not always suppressive, and this has recently been verified experimentally. We are currently working on an extension of the model that explicitly incorporates orientation tuning and selectivity, in order to investigate the mechanisms underlying orientation-specific center-surround interactions in V1. Our basic approach will be to incorporate feedback into a coupled hypercolumn model. The internal structure of each hypercolumn is idealized as a ring of orientation selective cells labeled by their orientation preference leading to the so-called coupled ring model of V1. We are also considering more complicated hypercolumn models that incorporate other feature preferences such as spatial frequency (eg. the spherical model of a hypercolumn). One important component of our work concerns the different classes of inhibitory interneurons (eg. horizontally projecting basket cells vs. vertically projecting local interneurons) and their role in contextual processing. Yet another aspect of our our work concerns how attentional modulation via feedback influences the responses to contextual stimuli.

Relevant publications

Cortical development

We are studying a variety of activity-based models for the development of the functional architecture of primary visual cortex. For example, we have recently constructed an activity-based developmental model of ocular dominance (OD) column formation in primary visual cortex that takes into account cortical growth. The resulting evolution equation for the densities of feedforward afferents from the two eyes exhibits a sequence of pattern forming instabilities as the size of the cortex increases, such that the mean width of an OD column is approximately preserved during the course of development. This is consistent with recent experimental observations of postnatal growth in cat. We are also investigating activity-based models for the joint development of OD columns and CO blobs that take into account the laminar structure of cortex. In yet other work we have extend the theory of self-organizing neural fields in order to analyze the joint emergence of topography and feature selectivity in primary visual cortex through spontaneous symmetry breaking. In particular we have shown how a two-dimensional isotropic topographic map can undergo a pattern forming instability that breaks the underlying rotation symmetry. This leads to the formation of elongated activity bumps consistent with the emergence of orientation preference columns. A particularly interesting property of the latter symmetry breaking mechanism is that the linear equations describing the growth of the orientation columns exhibits a rotational shift-twist symmetry, in which there is a coupling between orientation and topography.

Relevant publications

Geometric visual hallucinations and Euclidean shift-twist symmetry

In collaboration with Jack Cowan (University of Chicago) and Marty Golubitsky (University of Houston), we have developed a theory of geometric visual hallucinations based on the original idea of Ermentrout and Cowan that some disturbance such as a drug or flickering light can destabilize the visual part of the brain inducing a spontaneous pattern of cortical activity. The geometry of the resulting hallucination thus reflects the intrinsic architecture of the visual cortex. Our work has focused on a continuum model of V1 in which cells signal both the position and orientation of a local stimulus. Using symmetric bifurcation theory, we have shown that the cortical activity patterns underlying common visual hallucinations can be accounted for in terms of certain symmetry properties of the lateral connections, specifically, that they are invariant under the action of the planar Euclidean group - the group of rigid motions in the plane - rotations, reflections and translations. The resulting representation is twisted due to an anisotropy in the lateral connections, which tends to favor directions that are correlated with the orientation preferences of the interacting cells. More recently we have shown how spatially periodic correlations between the pattern of synaptic connections within V1 and cortical feature maps can induce a pinning of spontaneous activity patterns to the underlying feature maps. We have also been considering the role of Euclidean shift-twist symmetry in other areas of biology. For example, a wide variety of self-organizing biological systems exhibit aggregation and alignment phenomena. These occur spontaneously due to mutual interactions between the individual elements of a population, in which both the relative position and the relative orientation of the individuals has a significant effect on the nature of the interactions. Examples include the alignment of actin filaments within a cell's cytoskeleton, the alignment of mammalian fibroblast cells within the extracellular matrix, and the aggregation of animal social groups. We have shown how the aggregation and alignment of oriented objects in two dimensions can be modeled in terms of non-local population models, in which the underlying interaction kernel is invariant under the shift-twist action of the Euclidean group previously studied within the context of our continuum model of primary visual cortex.

Relevant publications

Noise-induced rhythmogenesis

A major area of study in neurobiology is understanding the dynamical mechanisms that underly the production of oscillations. One particularly interesting way rhythmic burst oscillations can arise is through a recurrently connected network of neurons possessing excitatory synapses and slow activity-dependent depression or adaptation. Such rhythms have been found in several brain areas including the Pre-Botzinger complex (PreBotC) and the developing chick spinal cord. The PreBotC is a rhythmogenic network in the mammalian brainstem thought to control the inspiratory phase of breathing. Cells in the PreBotC exhibit synchronized bursts of action potentials that together form a population-level oscillation with periods on the order from seconds to minutes. These rhythms persist in the absence of inhibition. A number of studies have focused on how intrinsic currents in a minority population of intrinsically rhythmic bursting, so called ``pacemaker" cells, could mediate population rhythmicity. More recently, however, there is evidence that pacemaker bursting cells may not be necessary for the production of the population rhythm, and it has been hypothesized that the rhythm is an emergent network property mediated by recurrent excitation. We have been studying an excitatory all-to-all coupled network of N spiking neurons with synaptically filtered background noise and slow activity-dependent hyperpolarization (AHP) currents. Such a system exhibits noise-induced burst oscillations over a range of values of the noise strength (variance) and level of cell excitability. Since both of these quantities depend on the rate of background synaptic inputs, we have shown how noise can provide a mechanism for increasing the robustness of rhythmic bursting and the range of burst frequencies. By exploiting a separation of time scales we have also shown how the system dynamics can be reduced to low-dimensional mean field equations in the large-N limit. Analysis of the bifurcation structure of the mean field equations provides insights into the dynamical mechanisms for initiating and terminating the bursts. In collaboration with Christopher Del Negro (College of William and Mary), we are currently extending our model to incorporate multiple time-scale AHP currents in order to provide a possible explanation for the experimentally observed peak in oscillation irregularity (maximal incoherence) for intermediate levels of excitability I. Such a mechanism is distinct from standard forms of coherence resonance.

Relevant publications

Traveling waves and breathers in excitable neural media

Analysis of the dynamical mechanisms underlying spatially structured activity states in neural tissue is crucially important for understanding a wide range of neurobiological phenomena, both naturally occurring and pathological. For example, neurological disorders such as epilepsy and migraine are characterized by waves propagating across the surface of the brain. Spatially coherent activity states are also prevalent during the normal functioning of the brain, encoding local properties of visual and auditory stimuli, encoding head direction and spatial location, and maintaining persistent activity states in short-term working memory. One of the important challenges in theoretical neurobiology is understanding the relationship between spatially structured activity states and the underlying neural circuitry that supports them. This has led to considerable recent interest in analyzing reduced biological models of synaptically coupled neuronal networks, in which the output activity of a neuron is taken to be a mean firing rate. Most analytical studies of these network models assume that the system is spatially homogeneous. However, we have recently shown that the combined effect of a spatially localized network inhomogeneity and recurrent synaptic interactions can result in nontrivial forms of spatially coherent oscillations (breathers) and waves. Such inhomogeneities could arise from external stimuli or reflect changes in the excitability of local populations of neurons. We are currently considering applications of our work to understanding the origins of epileptiform activity in a model of disinhibited neural tissue, and stimulus-induced coherent oscillations and phase-synchronization in a model of primary visual cortex.

Relevant publications

Spiking neuron models

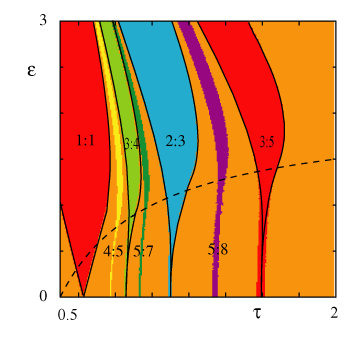
The dynamics of coupled oscillator arrays has been the subject of much recent experimental and theoretical interest. Example systems include Josephson junctions, lasers, oscillatory chemical reactions, heart pacemaker cells, central pattern generators and cortical neural oscillators. Most work in this area has been concerned with smoothly coupled oscillators under the assumption of weak interactions so that averaging methods can be used to reduce the system to a phase model. On the other hand, many oscillators in nature communicate via pulses. Examples include neural oscillators, fireflies, digital phase-locked loops and certain models of self-organized criticality. In collaboration with Steve Coombes (University of Nottingham), we have developed a theory of strong coupling instabilities in networks of integrate-and-fire (IF) neurons. An IF neuron fires a spike whenever its state variable reaches some threshold, and immediately after firing the state variable is reset to some zero resting level - the dynamics can thus be reduced to a nonlinear mapping of the firing times (threshold-crossing times) of the neurons. For sufficiently slow synaptic interactions the network behaviour is compatible with a corresponding firing rate model obtained by performing a short-term time-average of the IF dynamics. Our theory has been applied to a number of neural systems including swimming locomotion in Xenopus, orientation tuning in primary visual cortex, and wave propagation in excitable neural tissue. In related work, we have developed an integrate-and-fire model of propagating saltatory waves in active dendritic spines.

Relevant publications

For more information contact Paul C. Bressloff, 5-1633