

Never Divide by Zero
Division by zero is undefined, and for good reason. If we
assigned a number to the result of dividing by zero we'd run into
contradictions, and mathematics would become useless.
Let's approach the issue from several angles:
- Definition.
Division is the inverse process of multiplication. For example, the
unique (one and only) solution of
for
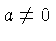 , is
When
, is
When 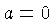 we get the equation
This
equation has no solution if
we get the equation
This
equation has no solution if 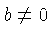 , and any number
, and any number 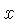 will be a
solution if
will be a
solution if 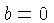 . In neither case do we have a unique solution.
This argument only shows that our usual way of defining division fails.
The next argument shows that there is no way of extending the definition in a way that does not give rise to contradictions.
. In neither case do we have a unique solution.
This argument only shows that our usual way of defining division fails.
The next argument shows that there is no way of extending the definition in a way that does not give rise to contradictions.
- A Contradiction. Suppose we define
for some real number
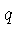 . Multiplying on both sides of the equation
gives
which is a contradiction (to
. Multiplying on both sides of the equation
gives
which is a contradiction (to 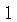 and 0 being different numbers).
and 0 being different numbers).
- A more subtle contradiction. Try to figure out what's
wrong with the following "proof" that
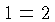 , before reading the answer
at the bottom of this page.
, before reading the answer
at the bottom of this page.
Let
Then
- Another Fallacy.
Temptations to divide by zero arise in subtle ways. For example,
consider the equation
The
routine approach to solving this equation begins by taking reciprocals
on both sides, giving
Multiplying with
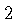 on both sides gives
Finally, adding
on both sides gives
Finally, adding 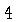 and
subtracting
and
subtracting 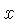 on both sides gives what might appear to be a
"solution":
.
on both sides gives what might appear to be a
"solution":
.
However, when we set 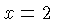 in
in 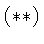 we divide by zero on both
sides of the equation and obtain nonsense. The equation
we divide by zero on both
sides of the equation and obtain nonsense. The equation 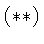 has
no solution!
has
no solution!
Of course, you would have discovered that fact by
following another one of our basic principles:
Always check your
answers.
The Moral of the Story
Whenever you divide by anything you should think about the possibility
of the divisor being zero. This should become a reflex like checking
your blind spot when you change lanes on the freeway. Usually there
is no problem, but if in fact there is somebody in your blind spot then the
consequences can be devastating, and you want to avoid the resulting
carnage!
The Answer to the Puzzle
In going from (3) to (4) we divide by zero since 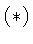 implies that
implies that 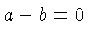 .
.


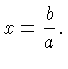
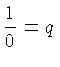
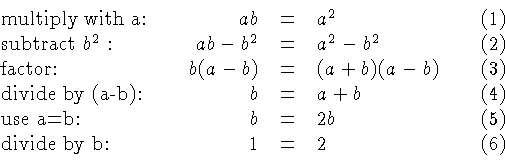
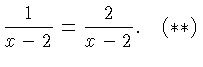
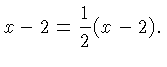
![]() in
in ![]() we divide by zero on both
sides of the equation and obtain nonsense. The equation
we divide by zero on both
sides of the equation and obtain nonsense. The equation ![]() has
no solution!
has
no solution!
![]() implies that
implies that ![]() .
.