Department of Mathematics --- College of Science --- University of Utah

Mathematics 1010 online

The Real Number Line

The Real Number Line

 

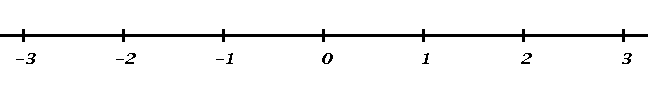
The real number system can be visualized as a horizontal line that extends from a special point called the Origin in both directions towards infinity. Also associated with the line is a unit of length. The origin corresponds to the number 0. A positive number x corresponds to a point x units away from the origin to the right, and a negative number -x corresponds to a point on the line x units away from the origin to the left. All of this is illustrated in the above Figure.

We said that the number corresponds to a point on the real number line, but actually there is no useful distinction between a real number and its corresponding point on the real number line. Hence we may also say that a real number is on the real line, and a point on the real number line is a real number.

We say that a number x is greater than a number y, in symbols

$\displaystyle x>y, $

if on the real number line x lies to the right of y. If we want to include the possibility that x is actually equal to y then we say that x is greater than or equal to y, and we denote this fact by

$\displaystyle x \geq y. $

For example,

$\displaystyle 3 > 2, \quad 3\geq 2, \quad 2\geq 2, \quad 1 > -100. $

Similarly, we say that x is less than y, in symbols

$\displaystyle x < y, $

if x lies to the left of y, and x is less than or equal to y, in symbols

$\displaystyle x \leq y, $

if x may be equal to y but no greater than y. For example,

$\displaystyle 2 < 3, \quad 2 \leq 3, \quad 2 \leq 2, \quad -100 < 1. $

Now get ready for a bit of convoluted logic that often confuses students in Math 1010.

A true statement such as

$\displaystyle 2 \geq 2 $

might surprise you since it's obviously not true that $ 2 $ is greater than $ 2 $. Things may be clearer if you pronounce the statement in words: $ 2 $ is greater than or equal to $ 2 $. The operative word here is or. A statement $ A~\hbox{or}~B $ is true in any of the following three cases:

$ 2 \geq 2 $ because $ 2 $ equals $ 2 $. That's one of the two parts of the meaning of $ \geq $. It may be tempting but would be wrong (false) to make the following statement: $ 2 \geq 2 $ is false since $ 2 $ is not greater than $ 2 $.

Here is another example. It is a true statement that Napoleon was a man or a woman because he was a man. The fact that he was not a woman does not make the statement false.

The utility of the symbol $ \geq $ is more apparent when we don't know the particular relationship. For example we may know that $ x\geq 2 $, even if we don't know whether $ x=2 $ or $ x > 2 $. Indeed, one major technique in mathematics to establish equality is to show separately that one quantity is greater than or equal to the other, and also that it is less than or equal to the other.

If x is less than y then we also say that x is smaller than y. For example, -25 is smaller than 2. Similarly we define the phrases larger, no smaller, and no larger.

The absolute value $ \vert x\vert $ of a real number x is its distance from the origin. If x is positive then $ \vert x\vert = x $ and if x is negative then $ \vert x\vert = -x $. (Remember that the negative of a negative number is positive.) So, for example,

$\displaystyle \vert 3\vert = \vert-3\vert = 3 $.

Slightly more subtle facts that you may want to ponder is that for all real numbers x and y

$\displaystyle \vert xy\vert = \vert x\vert\vert y\vert, \quad \vert x+y\vert \leq \vert x\vert + \vert y\vert $

and

$\displaystyle \vert x - y \vert \geq \big\vert \vert x\vert - \vert y\vert \big\vert. $

Hint: check this for all possible sign combinations of $ x $ and $ y $.

The distance between two real numbers x and y is the absolute value of their difference. For example, the distance between 3 and 5 is $ \vert 3-5\vert $ (i.e., 2) which makes perfect sense if you visualize this on the real number line. A more complicated example is provided by the distance d between 3 and -2. We have

$\displaystyle d = \vert 3 - (-2)\vert = \vert 3 + 2\vert = \vert 5\vert = 5. $

Again, this is consistent with the usual notation of distance a long a line.