

Originally the trigonometric functions were defined in the context of a right triangle. A more general definition can be given in terms of the unit circle. Using that approach also avoids getting stuck on the notion that those functions are defined only for angles up to 90 degrees.
So consider an angle t with its vertex at the origin, the initial side being the positive part of the horizontal axis, and the terminal side intersecting a circle of radius 1 centered at the origin, at a point (x(t),y(t)). Now, that's a mouthful! It's illustrated, however, and hopefully clearly, in this picture:

Clearly, the coordinates x and y are determined uniquely by the angle t.
There are three primary trigonometric functions, the sine, cosine, and tangent. They are abbreviated by sin, cos, tan and are defined by:
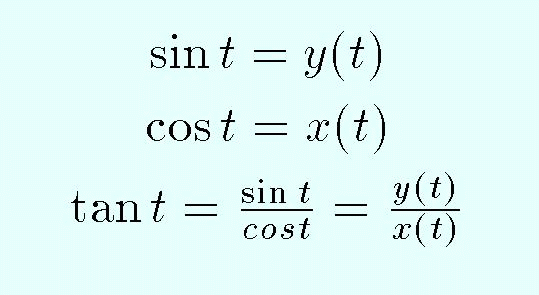
The reciprocals of these functions have also been given names, they are called the cosecant, secant, and cotangent, respectively, (abbreviated csc, sec, cot ). Thus
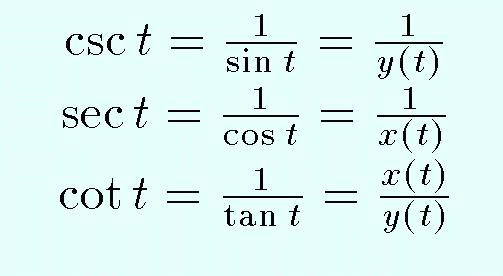
Only the first three matter, the others can always be replaced by the reciprocals of sin, cos and tan as needed. Indeed most calculators have keys only for these three functions.
Warning: You calculator is likely to have keys labeled

Those are keys for the inverse trig functions, not their reciprocal! Indeed. most calculators have keys only for the first three functions.
It's helpful to understand how the graphs of functions relate to their formulas. As an example, consider:

This is a scaled and shifted sine curve. Specifically,
Click anywhere in the following list to see the graphs of such and similar functions. For each example you'll see a page showing the graph and the Maple command that generated it. You can cut and paste that command into your own Maple session if you like.
Fine print, your comments, more links, Peter Alfeld, PA1UM
[04-Dec-2002]