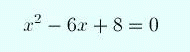Understanding Mathematics by Peter Alfeld, Department of Mathematics, University of Utah

An Example

Let's illustrate these ideas with an example based on a quadratic equation. In my experience, essentially the only thing you ever want to do with a quadratic equation is solve it.

So suppose we want to solve the equation

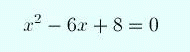(1)

A standard way of approaching this problem is to consider it a special case of the quadratic equation

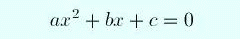(2)

where a=1, b=-6, and c=8, and then apply the formula

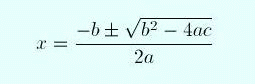(3)

That approach works and gives the right answer:

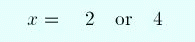(4)

However, it may fail in a number of ways: you may have forgotten the formula (3), or misremember it, misremember the meaning of a, b, and c, or make a mistake in evaluating the formula. In any of these cases you'll get no answer or the wrong answer, and there is no easy way to recover.

Here is a different way of solving the problem based on understanding. Forget about the formula (3), it's an example of clutter. (To this day I cannot remember it.) But since you understand these matters you know how the formula (3) was derived. You added a constant on both sides of the equation (2) that turned the left side of the equation into a perfect square. We can do this for the special case of equation (3). If the constant term was 9 instead of 8 we'd have a perfect square:

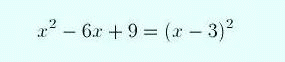(5)

If you understand that (and let's suppose for the moment you do) then it's clear after adding 1 on both sides of (1) that

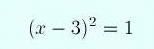(6)

and hence

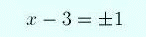(7)

That leads to the same solution as before:

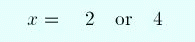(8)

So now suppose you did not understand how to complete the square. But you do know how the relevant formulas were derived. You looked at a square of a sum or difference, and just multiplied the two factors using the distributive law. Since there's a minus sign in (1) it makes sense to consider the square of a difference:

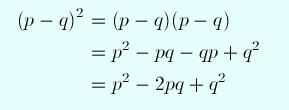(9)

You now have the formula you need. You just need to figure out that you need to set p=x and q=3 for the formula to be relevant.

The manipulation (9) can be explained in terms of simpler mathematics. It's based on the distributive law. That in turn can be explained in terms of boxes you draw on graph paper, and now we are down to the elementary level. Also present in (9) is the concept that we can use symbols instead of actual numbers, which typically is taught somewhere in grades 5 through 7. A fundamental principle applied in going from (1) to (6) via (5) is that an equation remains valid if we do the same thing (in this case adding 1) on both sides.

Obviously, this example is extremely simple. Its point is to illustrate the difference between an understanding based and a formula based approach to solving a problem. It's pretty clear that completing the square and rearranging things hardly takes more time - if any - than plugging the coefficients into the formula (3). On the other hand, it is independent of remembering formulas correctly.

In my experience, understanding the idea of completing the square encompasses the vast majority of what I need to understand about quadratic equations. Students would be well served if that's all they were taught, but with a view towards really and thoroughly understanding what they are doing. Click here to see an example of clutter in this context. All the things mentioned there can be derived by the student on his or her own if necessary.

Fine print, your comments, more links, Peter Alfeld, PA1UM

[16-Aug-1996]