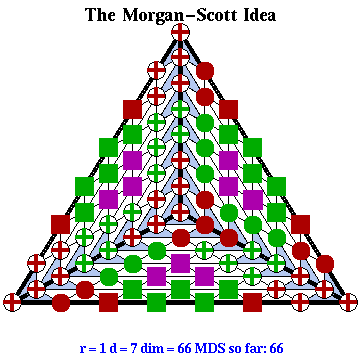

The main idea in the 1975 paper by Morgan and Scott can be paraphrased in terms of the Bernstein-Bézier form as follows:
Divide the domain points into sufficiently large globs around vertices and edges, and inside the interior of triangles such that the globs don't overlap. Then analyze the smoothness conditions first around vertices and then around edges. The situation is illustrated in the nearby Figure.
Globs around vertices are indicated in red, edge globs in green, and points in the interior of triangles in magenta. The radius of the vertex globs is 2, and each one of them can be analyzed locally as if it was the Bézier net on the vertex star for r=1 and d=2..
Once the vertex globs have been analyzed one can add the green points on each vertex and the green points on one side of that edge to the minimal determining set. Again, the analysis is strictly local. The magenta points are then also included.
For this approach to work the edge globs must have a radius
of r and the vertex globs must be large enough to
separate the edge globs. It turns out that they must have a
radius of 2r. The vertex globs themselves must not
overlap, and so the degree d must be greater than
4r.
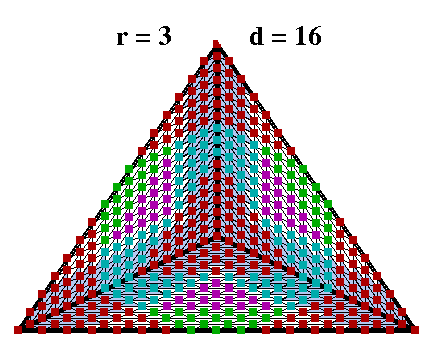
The above analysis is described in detail in papers 6, 7, and 10 . The analysis was later refined to give dimension statements for d > 3r+1, see papers 13 and 14.
As a further illustration consider the Figure nearby which shows the division of the domain points on the Clough-Tocher split for the case r=3 and d=16. Again, vertex globs are red and points deep in the interior of the triangles are magenta. For clarity the colors for globs around interior edges (Cyan) differs from those next to boundary edges (Green). The underlying gray shaded quadrilaterals show the extent of the smoothness conditions.
[15-Mar-1999]