Many Triangulations

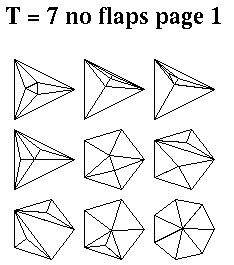
The MDS code has an experimental feature that lets you enumerate all triangulations of certain types. For example, the Figure nearby shows all possible triangulations with seven triangles having no flaps. (A flap is a triangle having exactly one interior edge. If you allow flaps there are 73 distinct triangulations with 7 triangles. )

Terms and Concepts

A triangulation has two components: its topology which describe how the triangles are connected, and its geometry which is the specification of the precise location of the vertices.

The enumeration mode of the MDS code attempts to compute all possible topologies of triangulations up to a certain number or size. It also has the ability to generate a particular geometry of each of these triangulations, and then display the triangulation and study spline spaces on them.

The original motivation for introducing this mode is that certain proof techniques require the analysis of a large number of particular triangulations with certain properties, and the first step for using these techniques is the ability to list these triangulations. However, using the enumeration mode one can conduct other interesting investigations as well.

In the context of the MDS code, an abstract triangulation is a set of triples of integers. We think of the integers as (abstract) vertices. Pairs of integers are (abstract) edges, and triples are (abstract) triangles. The order of the vertices in the triples is immaterial. Abstract triangulations are constructed recursively. A single triangle is an abstract triangulation. Given an abstract triangulation T, a new abstract triangulation can be obtained by adding a flap to T, or adding a fill. A flap is a new triangle one of whose edges occurs exactly once in the triangles of T. (I.e., the new triangle joins T on exactly one boundary edge.) The third point of the new triangle is not present in any triangle of T. (As a practical matter, it equals the highest index in T + 1). A fill is a new triangle two of whose edges occur exactly once in the triangles of T, and the third of whose edges does not occur at all among the triangles of T. (Since the two existing edges share a vertex on the new triangle they share the same vertex on the old triangulation.)

Two abstract triangulations S and T are isomorphic if T can be obtained by permuting the sequence of triangles and the labeling of vertices in S.

The MDS code proceeds by starting with a single triangle {0,1,2} and adding flaps and fills to form a growing list that contains all (non-isomorphic) abstract triangulations subject to certain constraints.

Invoking the Enumeration Mode

To use the enumeration features you need to download the MDS code. Select ENUMERATE as the last option of the triangulation menu on the MDS Control Panel.

User's Guide

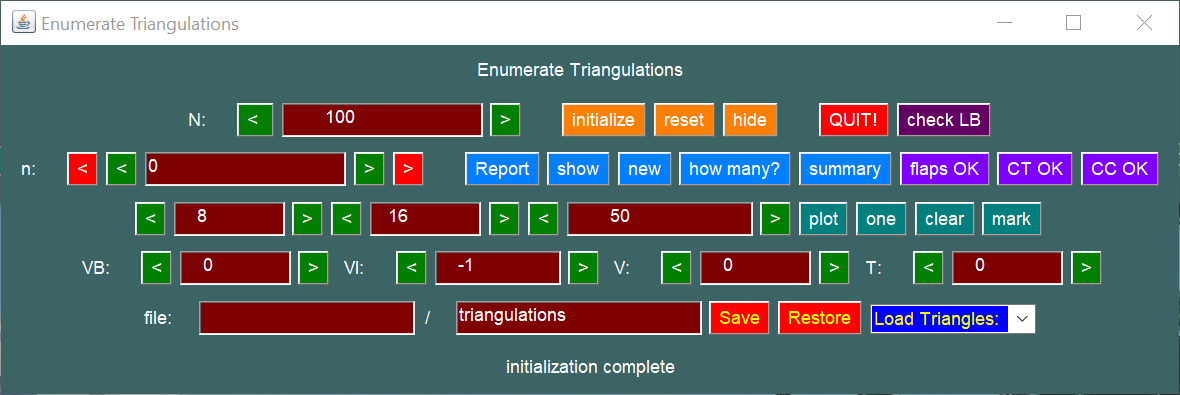
The image nearby shows the enumerate control panel. The controls have the following effects:

• Row 1
  • N: This textfield specifies the (maximum) number of triangulations to be computed.
  • initialize: This button generates the list of triangulations. This may take a long time, and once started it can't be interrupted.
  • reset: this button resets any constraints that have been imposed (see below).
  • hide: this button closes the enumerate control window. (To make it visible again reselect enumeration mode on the MDS Control Panel.)
  • Quit: this button dismisses the entire MDS package. Use with care.
  • check LB: an experimental feature that goes through the current list of triangulations and prints certain information to the standard output, including a statement of whether or not the dimension equals the lower bound. Best used by piping the standard output into a file and then examining the file with a text editor.
• Row 2
  • n: The textfield determines the index of the currently considered abstract triangulation. The green buttons increment or decrement that number. The red buttons do the same and in addition display a particular realization of the select abstract triangulation. Thus the code computes a particular geometry and displays it in the current drawing window. See below for a description of the particular geometry.
  • Report: Pressing this button causes a report to be listed to standard output. For example, the report on the Clough-Tocher split, with 0 being the interior vertex, and 1, 2, 3, being the boundary vertices, the report is:

     triangulation: VB = 3 VI = 1 no flaps
    tri.    v1     v2     v3
    0:       0      1      2
    1:       0      1      3
    2:       0      2      3
     Vertices:
    0: 300 300               <--- coordinates of vertex 0
    1: 541 300               <--- coordinates of vertex 1
    2: 180 500               <--- coordinates of vertex 2
    3: 180 100               <--- coordinates of vertex 3
    3 boundary edges:
    0: 1 2                   <--- vertices of boundary edge 0
    1: 1 3                   <--- vertices of boundary edge 1
    2: 2 3                   <--- vertices of boundary edge 2
    3 interior edges:
    0: 0 1                   <--- vertices of interior edge 0
    1: 0 2                   <--- vertices of interior edge 1
    2: 0 3                   <--- vertices of interior edge 2
    3 boundary vertices:
    0: 1  3 --- 2  3         <--- boundary vertex 0 has index 1, degree 3, neighboring vertices have indices 2 and 3
    1: 2  3 --- 1  3         <--- boundary vertex 1 has index 2, degree 3, neighboring vertices have indices 1 and 3
    2: 3  3 --- 1  2         <--- boundary vertex 2 has index 3, degree 3, neighboring vertices have indices 1 and 2
    1 interior vertices:
    0: 0  3                  <--- interior vertex 0 has degree 0 and degree 3
    

  • show: pressing this button will display a realization of the current abstract triangulation in the current drawing window. There it can be examined like any other triangulation.
  • new: has a similar effect as show, except it brings up a new drawing window.
  • how many: prints to the bottom row of the control window and to standard output the number of triangulations in the current list that satisfy the currently active constraints.
  • summary: prints a summary of the properties of the triangulations in the current list. For example, the summary for all triangulations with up to 12 triangles is:

     counting all 46281 triangulations (44669 have flaps)
     Number of triangulations:
     VB =      3     4     5     6     7     8     9    10    11    12    13    14
        VI
         0     1     1     1     3     4    12    27    78   214   654 1,944 5,767
         1     1     2     4    11    28    90   285   951 3,198 10,938            
         2     1     5    14    53   178   673 2,461 9,280                        
         3     4    18    69   293 1,187 4,919                                    
         4    16    88   396 1,845                                                
         5    78   489                                                            
    Number of Triangles:
         1     1
         2     1
         3     2
         4     5
         5     9
         6    28
         7    73
         8   239
         9   762
        10 2,659
        11 9,264
        12 33,238
    

    Thus 44,669 of the 46,281 triangulations have flaps, there are 2,659 triangulations with exactly 10 triangles, and there are 4,919 triangulations with 9 boundary vertices and 3 interior vertices.
  • flaps: determines whether triangulations with flaps are included in the summary, displayed in the drawing window, or plotted when required. The above summary with flaps not included becomes:

     not counting 44669 triangulations with flaps
     Number of triangulations:
     VB =      3     4     5     6     7     8     9    10    11    12    13    14
        VI
         0                                                                        
         1     1     1     1     1     1     1     1     1     1     1            
         2     1     3     4     8    12    23    39    75                        
         3     4    10    22    53   119   279                                    
         4    16    50   135   393                                                
         5    78   278                                                            
    Number of Triangles:
         1      
         2      
         3     1
         4     1
         5     2
         6     4
         7     9
         8    19
         9    51
        10   127
        11   372
        12 1,026
    

    Thus there are for example 75 different triangulations with 2 interior vertices, 10 boundary vertices, and no flaps.
  • CT OK: Similarly includes or excludes triangulations with Clough-Tocher vertices (i.e., interior vertices of degree 3).
  • CC OK: Similarly includes or excludes triangulations with cross cuts, i.e., interior edges both of whose vertices lie on the boundary. (Flaps are a special case of cross-cuts.)
• Row 3: Plotting. The items in this row control plotting sets of triangulations. The triangulations are plotted in m by n tables of entries each of which is k by k pixels. m, n, and k are controlled by the three textFields in this row, respectively. The entries of these textfields are limited by the available screen size. The buttons have the following effects:
  • plot: causes the plots to be generated, in as many windows as necessary, that show all triangulations satisfying the currently active constraints.
  • one: causes a plot of the current triangulation to be appended to the current plot.
  • clear: hides the current plotting windows
  • mark: adds or removes identifying numbers to the plot.
  Clicking with the left mouse button on any triangulation in the plot causes it to be displayed in the current drawing window. Clicking with the middle button causes it to be displayed in a new drawing window.
• Row 4: Constraints. The controls in this row impose constraints in addition to those specified by N, and the flaps and CT buttons.
  • VB: the number of boundary vertices. If it is zero there is no constraint. Otherwise all triangulation displayed must have VB boundary vertices. VB has no effect during initialization (since it may decrease by adding fills).
  • VI: similarly constrains the number of interior vertices.
  • V: constrains the total number of vertices. For display and summary the number of vertices must equal V, for initialization it must not exceed V.
  • T: similarly constrains the total number of triangles.
  All Constraints must be satisfied simultaneously.
• Row 5: Saving and restoring lists of triangulations. Initialization may take a long time. For example, finding all 169,062 triangulations with up to 13 triangles takes about two days of CPU time on my system. Therefore lists of triangulations can be stored in files. The file is specified by directory and file name and written or read by the Save and Restore button, respectively. Constraints are effective when saving. So for example you can save triangulations without flaps for further examination.

  It is possible to download files form our server directly into the MDS code running on your machine, using the menu in row 5. The following files are currently available:

  • T10: all triangulations with up to 10 triangles, 3,779 triangulations, 231,798 bytes.
  • T10.nf: all triangulations with up to 10 triangles but no flaps, 214 triangulations 12,770 bytes.
  • T11: all triangulations with up to 11 triangles, 9,264 triangulations, 648,484 bytes.
  • T11.nf: all triangulations with up to 12 triangles but no flaps, 372 triangulations 26,044 bytes.
  • T12: all triangulations with up to 12 triangles, 42,681 triangulations, 3,406,366 bytes.
  • T12.nf: all triangulations with up to 12 triangles but no flaps, 1,612 triangulations 116,786 bytes.
  • T13: all triangulations with up to 13 triangles, 169,062 triangulations, 13,472,680 bytes.
  • T13.nf: all triangulations with up to 13 triangles but no flaps, 4,821 triangulations 379,924 bytes.
  • T14: all triangulations with up to 14 triangles, 623,942 triangulations, 53,502,120 bytes. You need lots of memory, and lots of patience, to sift through these data.
  • T14.nf: all triangulations with up to 14 triangles but no flaps, 14,190 triangulations 1,204,396 bytes.
  You can also download these (binary) files directly through your browser. They may look empty, or as if they contain gibberish, but they should download normally.
• Row 6: Status Label. This labels provides some information. More is printed to standard output.

Downloading the Package

The entire package, containing all class files and triangulation lists, can be obtained by downlaoding the file

message

Copy that file to a directory on a Unix system and type

source message

Constructing the list of triangulations

The algorithm to construct the list of up to N triangulations reflects the fact that in multivariate spline research flaps are trivial. Thus within the constraints given by the size of the available stack (and possibly other constraints imposed on the number of triangles or vertices) fills are made whenever possible and flaps are added only when this is necessary to make fills possible. This principle is illustrated in the list of the first 100 triangulations so generated.

The following description of the algorithm assumes for simplicity that the list of triangulations is constrained only by the available space, i.e., the parameter N.

1. We are given a stack with N levels labeled from 0 to N-1. The stack is filled with triangulations starting from the bottom (at level 0).
2. The triangle [0,1,2] is put on the stack, and n = fill = flap = 0
3. While n < N-1
• Let T be triangulation flap on the stack.
• For each of the boundary edges of T:
  • Add a flap, to obtain a triangulation S. Check if S is a new triangulation. If so:
    • Increment n by 1.
    • Add S to the stack.
  • While fill < n
    • Let F be triangulation fill
    • For each of the boundary vertices of F:
      • Add a fill, denote the resulting triangulation by S, see if S is new, and if so, increment n and add S to the stack
    • Increment fill by 1.
• Increment flap by 1.

Determining Isomorphisms

As discussed above, two triangulations are isomorphic if one can be obtained from the other by relabeling the vertices and triangles and changing their sequence. Let S and T be two triangulations. The algorithm to compare them is as follows:

1. If T and S have different values of VB or VI they are not isomorphic
2. The vertices of T and S are ordered by increasing degree. If two corresponding vertices have different degrees then S and T are not isomorphic.
3. Now the real work starts.
   • Divide both sets of triangles (from S and T) into equivalence classes. Two vertices are equivalent if they have the same degree and they are both boundary or both interior vertices. Two triangles are equivalent if their vertices form three equivalent pairs.
   • If the two triangulations do not have identical equivalence classes they are not isomorphic.
   • Try to rearrange the triangles in T so as to duplicate the construction of S. Create a stack of triangles in T.
   • If the stack is full S and T are isomorphic, if it's empty they are not.
   • Put a triangle from the of the same class as triangle 0 in S on the stack.
   • Until the stack is full or empty:
     • The triangles currently on the stack are consistent if vertices in triangles on the stack always correspond to the same vertices of the corresponding triangles in S.
     • Add a triangle of the right class to the top of the stack. Check that consistency is maintained.
     • If that's not possible check if it's possible to relabel the vertices of the top triangle and still have consistency.
     • If that's not possible, remove the top triangle.

In computing all triangulations up to 13 triangles, the last step (involving the stack of triangles) never identified two triangulations as distinct that have not already been recognized as such at this stage. If you find two non-isomorphic triangulations that have passed all tests up to this stage the package will inform you and I'd be very interested to hear from you.

Rendering an Abstract Triangulation

The particular geometries displayed in the plotting windows are obtained by arranging the boundary vertices equally spaced in the proper sequence in a circle and then computing coordinates of interior vertices such that each interior vertex is the average of all vertices connected to it by an edge.

Examples

The following table lists the number of triangulations with a given number of boundary vertices (VB) and interior vertices (VI), and no flaps. Clicking on a link will show a picture of these triangulations. Columns correspond to VB, rows to VI. The values for VI=0 (no triangulations without flaps) and VI=1 (one triangulation for each VB) are not shown.

The following table similarly lists the numbers of triangulations including flaps, with a given value of VB and VI, and up to 13 triangles.

Literature

This chapter is under construction.

[31-Jan-2003]