This page describes the two best known and most famous unsolved problems in bivariate splines.
Let S be our ordinary spline space with
r=1 and d=3
This space is of great interest for applications because it provides the smallest polynomial degree for which the dimnesnion of S always exceeds the number of vertices in the triangulation. Thus one can hope to be able to interpolate to given function values at the vertices of the triangulation.
As an exercise you may want to show that
dim S > 3VB + 2 VI + sigma (*)
where
It is widely conjectured that actually
dim S = 3VB + 2 VI + 1 + sigma (**)
If you can prove this statement (or find a counterexample, perhaps with the MDS applet above) you will be instantly famous, at least among the people who care about multivariate spline spaces!
So what's the difficulty? It's hard to localize things. All kinds of apparently obvious induction arguments fail because whatever you do in one triangle affects what happens everywhere else. The main difficulty seems to be that adding triangles can actually decrease the dimension of S. For example, adding a fill, i.e., joining a new triangle on two edges to the triangulation, increases VI by 1 and decreases VB by 1. Thus the conjectured dimension decreases by 1.
I have recently been looking into the possibility of using
techniques for proving (**) that were developed for the
solution of the famous Four Color Map problem. You can
examine slides of a recent talk
on this connection.

Another famous open question is
Is it always possible to find a function in S that assumes given values at the vertices of the triangulation?
In other words, is it possible for all triangulations and all sets of function values to interpolate at the vertices of the triangulation? At first it seems obvious that this must be possible since the dimension of S exceeds twice the number of vertices. But it is conceivable, even though no such case is known, that for some triangulations the interpolation conditions and the smoothness conditions are inconsistent.
One way of approaching a proof of (**) is to be a little
more specific and try to prove that one can always set 3
coefficients at and around a boundary vertex, 2 at and
around an interior vertex, and then determine the whole
space by imposing one more point, e.g., the central control
point of a particular triangle. The advantage of making the
stronger statement is that for an induction proof one has a
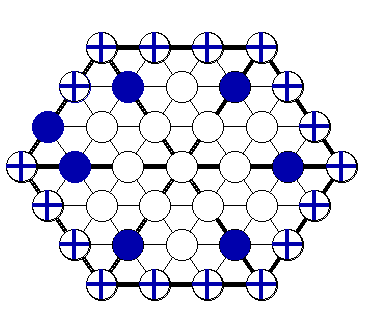
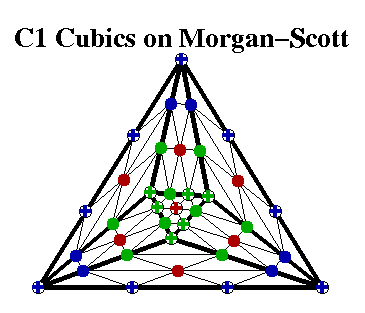
stronger induction hypothesis to work with. The Figures on
this page nearby show several attempts in that direction,
with blue domain points around boundary vertices, green
points around interior vertices, and the final point (and
the points implied by it) being red.
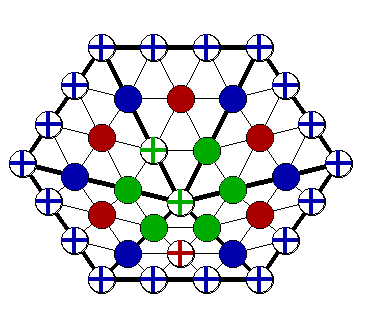
It turns out that this approach works on the Morgan-Scott split, and on a generic hexagon, but not on a regular hexagon, as indicated by the Figures! On the regular hexagon three points are imposed on every boundary vertex except the one on the very left. In the 1-disk around that vertex only two points can be imposed (after imposing three points around each of the other boundary vertices).
Here is summary of what is and is not known about S:
[15-Mar-1999]