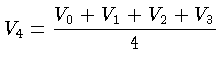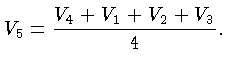Macro Elements on the double Clough-Tocher Split
The Clough-Tocher Macro Panel lets you impose symmetric
super smoothness conditions on the Clough-Tocher split and then check if
a macro element can be built with those conditions.
To obtain the macro panel select the configuration "Clough-Tocher",
and clock on the button "macro elements" in the control panel.
The buttons on the macro panel have the following effects:
- Hide cause the macro panel to disappear. To make it
reappear click again on "macro elements".
- Draw causes the current smoothness conditions to be drawn
initially, or if the linear algebra in the drawing window has been
initialized. (Otherwise the smoothness conditions are drawn
automatically whenever they are changed.)
- Init initializes the linear algebra (and exits super
selection mode) in the drawing window.
- Set initializes the linear algebra if necessary and
attempts to set the natural data that go with the current set of
smoothness conditions and the current polynomial degree.
- Clear removes all super smoothness conditions.
- The status window gives information about the current analysis in
some situations.
Super smoothness conditions can be imposed using the text fields
in the second row of the macro panel, and the buttons to either side
of those text fields. The text fields lists the additional
degree of smoothness. So if all the text fields show zero then
the spline is the ordinary space without super smoothness conditions
at all.
The types of smoothness conditions that can be imposed are listed
below. To understand the labels on the macro panel recall the
labeling of the vertices: 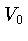 ,
, 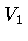 ,
, 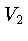 , and
, and 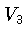 are
the boundary vertices,
are
the boundary vertices,
is
the centroid, and 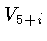 is the subcentroid opposite
is the subcentroid opposite 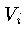 ,
, 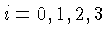 . For example,
The phrase "
. For example,
The phrase "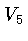 " below refers to super smoothness at all four
subcentroids, and
" below refers to super smoothness at all four
subcentroids, and 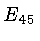 refers to super smoothness along edges for
the centroid the subcentroid since
refers to super smoothness along edges for
the centroid the subcentroid since 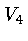 is the centroid, and
is the centroid, and
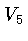 is a subcentroid.
is a subcentroid.
The following groups of super smoothness conditions are available:
Natural Data
The natural data are the same as for the single Clough-Tocher split.
C2 Macro Schemes
The following links let you explore the possibility of constructing a
C2 macro scheme of degree 9.
![]() ,
, ![]() ,
, ![]() , and
, and ![]() are
the boundary vertices,
are
the boundary vertices,