Owen Lewis

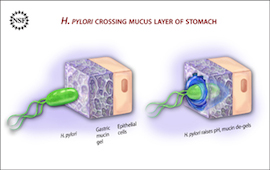
In general, my research interests involve using the techniques of Mathematics to explore how the laws of Physics inform Biological function. Specifically, I am interested in the mechanics of fluids and complex fluids, as well as transport processes therein. My mathematical training focuses on techniques for solving Partial Differential Equations, as well as Numerical methods for complex materials. I have worked on developing an Immersed Boundary (IB) method for poro-elastic materials in the context of cellular modelling, as well as time-integration of electro-diffusion equations in a two-phase media model of gastric mucus. I have also developed models of strain relaxation in filamentous actin networks in emmulsion droplets.

My current research is focused on using mathematical models to explain how the gastric mucus layer protects the stomach wall. I am exploring how the mechanics and rheology of the mucus itself interact with the electro-chemistry of stomach acid to create a protective barrier. This barrier has the physiological task of protecing the stomach wall from acid, digenstive enzymes, and infection by various pathogens. Broadly, this project involves investigation of the mechanics of hydrated polymeric gels, as well as elecro-diffusive transport within complex media.

An ongoing project started during my dissertation focuses on analytical and numerical models of cytoplasmic streaming witnessed in the slime mold Physarum. This work is performed in conjunction with Toshi Nakagaki, as well as the lab of Juan Carlos del Alamo. Through the comparison of modeling predictions to traction stress microscopy and particle image velocimetry data, we explore the coordination of spatiotemporal waves necessary to drive cellular motility through cytoplasmic pumping.