Math 2250-3

Numerical Computations

Wednesday, Sept 13, 2000

In this handout we will study numerical methods for approximating solutions to first order differential equations. (The fact is, most differential equations do NOT have simple formulas for their solutions, despite all the examples you've seen in which they do. In the case that no nice formula exists for the solution one must approximate it numerically.) A month from now we will see how higher order differential equations can be converted into first order systems of differential equations, and that there is a natural way to generalize what we are doing now in the context of a single first order differential equation to this more complicated setting. So understanding today's material will be an important step in understanding numerical solutions to higher order differential equations and to systems of differential equations.

We will be working through selected material from sections 2.4-2.6 of the text.

The most basic method of approximating solutions to differential equations is called Euler's method, after the 1700's mathematician who first formulated it. If you want to approximate the solution to the initial value problem dy/dx = f(x,y), y(x0)=y0, first pick a step size ``h''. Then for x between x0 and x0+h, use the constant slope

f(x0,y0). At x-value x1:=x0+h your y-value will therefore be y1:=y0 + f(x0,y0)h. Then for x between x1 and x1+h you use the constant slope f(x1,y1), so that at x2:=x1+h your y-value is y2:=y1+f(x1,y1)h. You continue in this manner. It is easy to visualize if you understand the slope field concept we've been talking about; you just use the slope field where you are at the end of each step to get a slope for the next step. It is straightforward to have a programmable calculator or computer software do this sort of tedious computation for you. In Euler's time such computations would have been done by hand!

A good first example to illustrate Euler's method is our favorite DE from the time of Calculus, namely dy/dx =y, say with initial value y(0)=1, so that y=exp(x) is the solution. Let's take h=0.2 and try to approximate the solution of the x-interval [0,1]. Since the approximate solution will be piecewise affine, we only need to know the approximations at the discrete x values x=0,0.2,0.4,0.6,0.8,1. Here's a simple ``do loop'' to make these computations.

> restart: #clear any memory from earlier work

> x0:=0.0; xn:=1.0; y0:=1.0; n:=5; h:=(xn-x0)/n;
#specify initial values, number of steps, and size

> f:=(x,y)->y; #this is the slope function f(x,y)
#in dy/dx = f(x,y), in our example dy/dx = y.

> x:=x0; y:=y0; #initialize x,y for the do loop

> for i from 1 to n do

> k:= f(x,y): #current slope, use : to suppress output

> y:= y + h*k: #new y value via Euler

> x:= x + h: #updated x-value:

> print(x,y,exp(x)); #display current values,

> #and compare to exact solution.

> od: #``od'' ends a do loop

Notice your approximations are all a little too small, in particular your final approximation 2.488... is short of the exact value of exp(1)=e=2.71828.. The reason for this is that because of the form of our f(x,y) our approximate slope is always less than the actual slope. We can see this graphically using plots:

> with(plots):with(linalg):

> xval:=vector(n+1);yval:=vector(n+1); #to collect all our points

> xval[1]:=x0; yval[1]:=y0; #initial values

> #paste in the previous work, and modify for plotting:

> for i from 1 to n do

> x:=xval[i]: #current x

> y:=yval[i]: #current y

> k:= f(x,y): #current slope

> yval[i+1]:= y + h*k: #new y value via Euler

> xval[i+1]:= x + h: #updated x-value:

> od: #``od'' ends a do loop

> approxsol:=pointplot({seq([xval[i],yval[i]], i=1..n+1)}):

> exactsol:=plot(exp(t),t=0..1,`color`=`black`):

> #used t because x was already used above

> display({approxsol,exactsol});

If you connect the Euler dots in your mind, the picture above is like the one in figure 2.4.3, on page 109 of the text. The upper graph is of the exponential function, the lower graph is of your Euler approximation. The reason that the dots lie below the true graph is that as y increases the slope f(x,y)=y should also be increasing, but in the Euler approximation you use the slope at each (lower ) point to get to the next (higher) point.

It should be that as your step size ``h'' gets smaller, your approximations get better to the actual solution. This is true if your computer can do exact math (which it can't), but in practice you don't want to make the computer do too many computations because of problems with round-off error and computation time, so for example, choosing h=0.0000001 would not be practical. But, trying h=0.01 should be instructive:

Since the width of our x-interval is 1, we stepsize h=0.01 by taking an n-value of subintervals to be100. We keep the other data the same as in our first example. The following code only prints out approximations when h is a multiple of 0.1:

> x0:=0.0; xn:=1.0; y0:=1.0; n:=100; h:=(xn-x0)/n;

> x:=x0; y:=y0;

> for i from 1 to n do

> k:= f(x,y): #current slope

> y:= y + h*k: #new y value via Euler

> x:= x + h: #updated x-value:

> if frac(i/10)=0

> then print(x,y,exp(x));

> fi; #use the ``if'' test to decide when to print;

> #the command ``frac'' computes the remainder

> #of a quotient, it will be zero for us if i

> #is a multiple of 10.

> od:

We can also see this graphically:

> xval:=vector(n+1);yval:=vector(n+1); #to collect all
#our points

> xval[1]:=x0; yval[1]:=y0; #initial values

> #paste in the previous work, and modify for plotting:

> for i from 1 to n do

> x:=xval[i]: #current x

> y:=yval[i]: #current y

> k:= f(x,y): #current slope

> yval[i+1]:= y + h*k: #new y value via Euler

> xval[i+1]:= x + h: #updated x-value:

> od: #``od'' ends a do loop

> approxsol:=pointplot({seq([xval[i],yval[i]], i=1..n+1)}):

> exactsol:=plot(exp(t),t=0..1,`color`=`black`):

> #used t because x was already used above

>

> display({approxsol,exactsol});

Actually, considering how many computations you did with n=100 you are not so close to the exact solution. In more complicated problems it is a very serious issue to find relatively efficient ways of approximating solutions. An entire field of mathematics, ``numerical analysis'' deals with such issues for a variety of mathematical problems. The book talks about some improvements to Euler in sections 2.5 and 2.6. If you are interested in this important field of mathematics you should read 2.5 and 2.6 carefully. Let's summarize some highlights below.

For any time step h the fundamental theorem of calculus asserts that, since dy/dx = f(x,y(x)

> restart:

> y(x+h)=y(x) + Int(dy/dt,t=x..x+h);

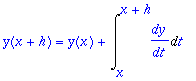
> y(x+h)=y(x) + Int(f(t,y(t)),t=x..x+h);

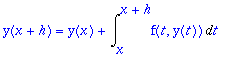
The problem with Euler is that we always approximated this integral by h*f(x,y(x)), i.e. we used the left-hand endpoint as our approximation of the ``average height''. The improvements to Euler depend on better approximations to that integral. ``Improved Euler'' uses an approximation to the Trapezoid Rule to approximate the integral. The trapezoid rule for the integral approximation would be (1/2)*h*(f(x,y(x))+f((x+h),y(x+h)). Since we don't know y(x+h) we approximate it using unimproved Euler, and then feed that into the trapezoid rule. This leads to the improved Euler do loop below. Of course before you use it you must make sure you initialize everything correctly. We'll compare it when n=5, to our first (unimproved) attempt.

> x0:=0; y0:=1;xn:=1.0;n:=5;
h:=(xn-x0)/n;
x:=x0; y:=y0;
f:=(x,y)->y;

> for i from 1 to n do

> k1:=f(x,y): #left-hand slope

> k2:=f(x+h,y+h*k1): #approximation to right-hand slope

> k:= (k1+k2)/2: #approximation to average slope

> y:= y+h*k: #improved Euler update

> x:= x+h: #update x

> print(x,y,exp(x));

> od:

>

Notice we almost did as well with improved Euler when n=5 as we did with n=100 in unimproved Euler.

One can also use Taylor approximation methods to improve upon Euler; by differentiating the equation dy/dx = f(x,y) one can solve for higher order derivatives of y in terms of the lower order ones, and then use the Taylor approximation for y(x+h) in terms of y(x). See the book for more details of this method, we won't do it here.

In the same vein as ``improved Euler'' we can use the Simpson approximation for the integral instead of the Trapezoid one, and this leads to the Runge-Kutta method which is widely used in real software.

(You may or may not have talked about Simpson's Rule in Calculus, it is based on a quadratic approximation to the function f, whereas the Trapezoid rule is based on a first order approximation.) Here is the code for the Runge-Kutta method. The text explains it in section 2.6. Simpson's rule approximates an integral in terms of the integrand values at each endpoint and at the interval midpoint. Runge-Kutta uses two different approximations for the midpoint value.

.

> x:=x0; y:=y0; n:=5; h:=(xn-x0)/n;

> for i from 1 to n do

> k1:=f(x,y): #left-hand slope

> k2:=f(x+h/2,y+h*k1/2): #1st guess at midpoint slope

> k3:=f(x+h/2,y+h*k2/2): #second guess at midpoint slope

> k4:=f(x+h,y+h*k3): #guess at right-hand slope

> k:=(k1+2*k2+2*k3+k4)/6: #Simpson's approximation for the integral

> x:=x+h: #x update

> y:=y+h*k: #y update

> print(x,y,exp(x)); #display current values

> od:

>

Notice how close Runge-Kutta gets you to the correct value of e, with n=5.

Even with code like Runge-Kutta there are subtleties and problems which particular problems will cause. We will not go into those here; there are good examples in sections 2.4-2.6 and the homework problems.