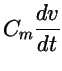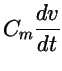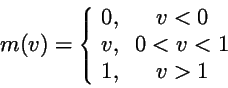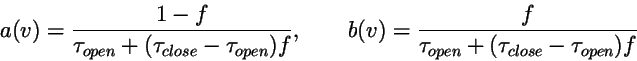

Next: Tyson-Fife
Up: Two_variable_models
Previous: Mitchell-Schaeffer
To make the Mitchell-Schaeffer look more like a cardiac ionic model, take
where
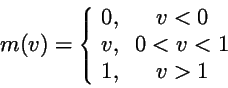 |
(25) |
To match the M-S model, we take
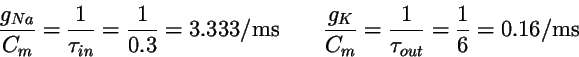 |
(26) |
We also take
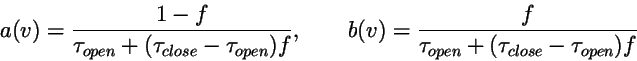 |
(27) |
where
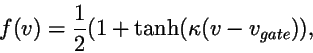 |
(28) |
so that
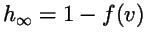 , and
, and
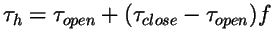 . If
. If
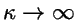 , this reduces exactly to the M-S model. In the M-S model,
, this reduces exactly to the M-S model. In the M-S model,
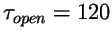 ms,
ms,
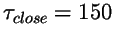 ms, and
ms, and
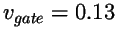 .
.
Movie