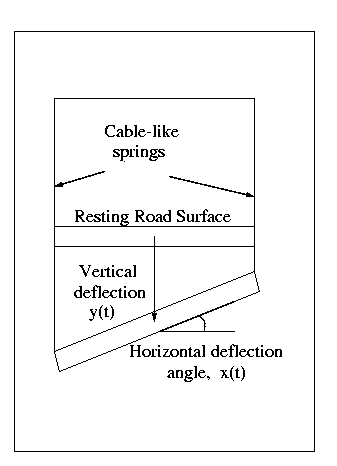
Small oscillations and engineering implications


After the collapse of the Tacoma Narrows bridge, an engineering analysis determined that the section of the bridge formed by the roadway and the large thick supports on its side, called stiffening-plate girders, did not absorb the turbulence of wind gusts. At the same time, the narrow two-lane roadway gave the bridge span a high degree of flexibility.

Mathematically, modeling the bridge as a function of space and time can lead to complicated equations. The figure to the right schematically shows the vertical deflection y(t) and the horizontal deflection angle x(t).

The simplest model uses Newton's second law. The model assumes the cables supporting the road surface behave like Hooke's law springs. Then

x'' + c x' + k x = f(t)

where c>0 is the coefficient of viscous damping divided by the mass, k is the Hooke's spring constant of the cables divided by the mass, and f(t) is the acceleration of the bridge due to the wind.

The vertical displacement y(t) is also governed by a second order constant coefficient linear differential equation y''(t)+cy'(t)+(k/3)y(t)=g, where g is the acceleration due to gravity.

The equations are known to also model mass-spring-dashpot systems, a pendulum for small displacements and LRC-electrical circuits.

The project studies the effects of viscous damping and forcing;  k is given and choices are made for c and f(t).

The engineers recognized that in this equation, if c were large enough, the viscous damping would prevent oscillations from growing very large. To implement this in bridges, the engineers replaced the stiffening-plate girders with web trusses in future bridges. The differences are shown in the figure below; the old bridge is on the left and the new bridge is on the right.

Go on to the next section