Math 4800 S16 — Network Inverse Problems
Class Information
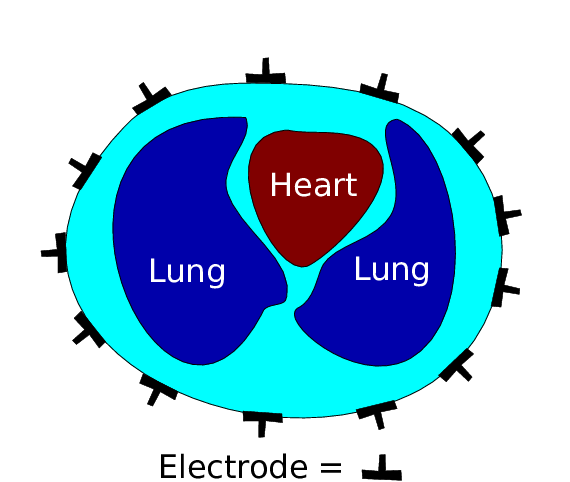
- Description: Networks can be used to model many physical phenomena such as electricity conduction and vibrations of an elastic body. We focus on the inverse problem, i.e. the question: Can one recover properties of the network from measurements made at a few nodes? A classic example is to recover the position and weight of beads in a vibrating string from measuring how the string responds to being plucked at one end. This class explores connections between physics, graph theory, partial differential equations, linear algebra and stochastic processes. Applications include medical imaging and geophysical prospecting.
- When and Where: Tue and Tue, 9:10-10:30am, JTB 110 (3 credits)
- Instructor: Fernando Guevara Vasquez (fguevara (AT) math (DOT) utah (DOT) edu, JWB 330, 801-581-6131)
- Prerequisites: Permission of the instructor.
Linear Algebra is a must. Programming, PDEs and/or Foundations of Analysis I
are highly desirable.
- Flyer: flyer.pdf
Syllabus
A detailed syllabus is TBA
Topics include:
- Network models (resistor networks, elastodynamic networks, acoustic networks)
- The graph Laplacian
- Spectral properties
- The Dirichlet problem
- The Dirichlet to Neumann map
- Connections with random walks on graphs
- The p-Laplacian on graphs
- The discrete string problem: can one hear the positions of beads and their
weight on a string? (connection with Lanczos method, Gaussian quadrature and
optimal grids)
- The inverse problem for resistor networks
- Connecting the continuum and discrete inverse problems
- Other inverse problems on networks