Multiphase mixtures

Best structures of multiphase composites are mainly unknown.

Dealing with multiphase composites and polycrystals one needs to consider a much greater variety of topologically different microstructures. Some results are discussed here, but the whole picture is not clear yet. The multicomponent optimal structures often have fractal geometries. The same geometric construction is repeated again and again as in an Escher picture

The difference between two-phase and multi-phase optimal structures is as huge as the difference between the black-and-white and the color TV. For detailed discussing, we refer to Variational methods for Structural Optimization Chapter 12.

Here, we restrict ourselves with two remarks that show the complexity of the problem.

1. The laminate is a structure in which the fields are constant in each material. A laminate is the only type of a two-component structure with these properties. For multi-component structures, the constancy of the fields corresponds to large class of ``T-structures''

A example of ``T-structure''

2. The next picture shows the variety of the topology of optimal isotropic conducting two-dimensional three materials structure. Note the optimal topology of two-material mixtures us pretty clear: "good" material outside, "bad" material inside inclusions. In contrast, the optimal topology of three-component mixtures depend on their volume fractions. \begin{rawhtml} Isotropic structure of the best conductivity.

Large volume fraction of the best material, the swiss cheese topology (Milton, 1986)

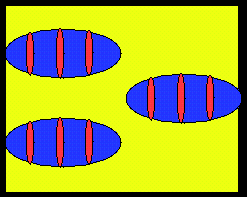Small volume fraction of the best material; this material localizes inside the inclusion to compensate the properties of the worst material (Cherkaev, 1998)

Red color corresponds to the best conductor, yellow color - to the intermediate conductor, blue color - to the worst conductor.