G-closure

What is the G-closure?

The set of effective properties of all possible structures made from given materials
is called G-closure of the set of the materials' properties.

The set of effective properties of all possible structures made from given materials
taken in given proportions p is called G-p-closure of the set of original properties.

Why are we interested in the G-closures?

G-closure shows what effective properties may has a composite assembed from given materials.
The boundary of the G-closure does not depend on structure of the composite, only on the properties of materials in the composition. Sometimes, it is described by a simple analytical formula.
The microstructures that realiaze the boundary points are optimal in the sense that they correspond to extremal overall properties.

Examples

The following picture shows the G-closure for two conducting materials and the best structures that correspond to boundaries of the G-closure.

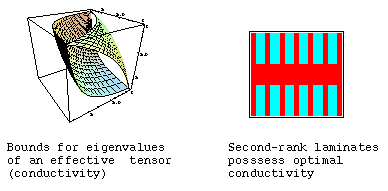
Mathematically, the problem of bounds and of extremal structures can be formulated as a nonconvex variational problem of minimization of the sum of energies/complimentary energies that a structure stores under different loadings.
We have now a pretty detailed picture of structures of two-phase conducting and elastic materials, but the best structures of multiphase composites are mainly unknown.

Multiphase mixtures
The difference between two-phase and multi-phase optimal structures is huge. It is similar to the difference between the black and white and the color TV or between flat and spacial imaging.
The optimal microstructures of multicomponent mixtures are mostly unknown, altough several problems are already solved. The structural variety and the difficulty of the problems are significantly higher then of the two-materials mixtures.
Jumping from two-material structures to multimaterial is like passing from plane to three-dimensional world or passing from black-and-white to color TV.
The next pictures show the variety of the topology of optimal isotropic conducting two-dimensional three materials structure. Note the optimal topology of two-material mixtures us pretty clear: "good" material outside, "bad" material inside inclusions. In contrast, the optimal topology of three-component mixtures depend on their volume fractions.

Isotropic structure of the best conductivity.
Red color corresponds to the best conductor, yellow color - to the intermediate conductor, blue color - to the worst conductor.

Large volume fraction of the best material, the swiss cheese topology (Milton, 1986)

Small volume fraction of the best material; this material localizes inside the inclusion to compensate the properties of the worst material (Cherkaev, 1998)

Back to the Main page