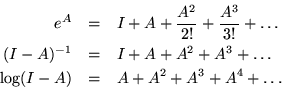Example: $\sin$ of a matrix

What is $\sin$ of a matrix?

The classical(geometrical) definition of $\sin$ is as follows:

For an angle $x$ (that is for a real number $x$ that lies between 0 and $\pi/2$) $\sin$ is the ratio

$$\sin(x)=a/c$$

where $a$ is the opposite side and $c$ is the hypotenuse of the right triangle with the angle $x$. \hr

Clearly, this definition cannot be expanded to incorporate matrices or complex numbers instead of angles.

Universal definition

Also, the function $\sin$ can be defined by the Taylor series:

$$\sin x = x - {x^3 \over 3!} + {x^5 \over 5!}-{x^7 \over 7!} + \ldots$$

This definition returns the same value of $\sin$ as the classical definition everywhere where the last one is applicable, but the definition through the Taylor series is applicable to a broader set of arguments.

sin of a complex argument

Now one can compute $\sin$ of any real or complex number. Particularly, one can easily prove the selebrated Euler's formula

$$e^{i x}= \cos(x) + i \sin(x)$$

and other trigonometric formulas for complex numbers, expanding the definition of trigonometric functions.

Notice that $\sin(x)$ does not need to be smaller than one any more; on the contrary, the equation

$$\sin(x) =N$$

where $N$ is any real or complex number has a solution in the complex plane.

sin of matrices

Recall, that the Taylor series uses only a sequence of additions and multiplications to define a function. These operations are well defined for any square $n \times n$ matrix $A$, where $n$ is an arbitrary integer. Therefore, we have

$$\sin A = A - {A^3 \over 3!} + {A^5 \over 5!}-{A^7 \over 7!} + \ldots$$

Now we may prove all trigonomeric formulas for matrix arguments or investigate the transform of eigensystem of a matrix.

Similarly, we can define any other analytic function of a square matrix $A$:

$$\begin{eqnarray*} e^A & = & I + A + {A^2 \over 2!} + {A^3 \over 3!}+ \ldots \\ ... ...}+ \ldots \\ \log (I - A) & = & A + A^2 + {A^3 }+ A^4 + \ldots \end{eqnarray*}$$

and so on.