


Next: Distributions and weak limits:
Up: ``Strange'' limits
Previous: ``Strange'' limits
Consider a sequence:
When
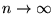 , the sequence converges to the so-called
, the sequence converges to the so-called 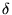 -function (which, by the way, is not a
function but a new object: The distribution).
-function (which, by the way, is not a
function but a new object: The distribution).
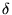 -function equals zero if
-function equals zero if 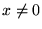 , is infinitely large if
, is infinitely large if 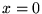 ,
and, additionally, keeps the area under its graph equal to one. This last
extra requirement differs
,
and, additionally, keeps the area under its graph equal to one. This last
extra requirement differs 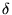 -function from ``normal'' functions. It comes
from the constancy of the integrals
-function from ``normal'' functions. It comes
from the constancy of the integrals
Problem: Prove the basic propety of the 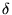 -function
-function
for all smooth functions 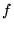 .
.
Andre Cherkaev
2001-11-16
![]() -function
-function