Paradoxes and Expansions

The tremendously complex world of today's mathematics makes us wonder about its genesis and rules of its creation. Here we show several ways of growing of mathematical subjects.

Mathematicians love to think about problems without solutions. To solve the paradox, one usually extends the notion of solution. Since the solutions of math problems are numbers or functions, the expansion leads to generalizing of definition of them.

For example, consider an ``incorrect'' system of two equations that does not have a solution:

$$\left\{ \matrix{ x=0\cr x=2.} \right.$$

Depending on the origin of the problem, one may consider an expansion of the very definition of what ``solution'' is:

• A ``solution'' 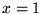$x=1$ is the best approximation or compromise between two contradictory requirements.
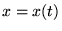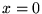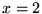• A ``solution'' $x= x(t)$ can be a function that alters between the values $x=0$ and $x=2$ infinitely fast.
• A ``solution'' 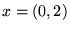$x= (0, 2)$ can be a vector: Its first component satisfies the first equation, and its second component satisfies the second equation.

Besides, one should examine the adequateness of the modeling or logic of derivation of the contradictory system.