Molecular mechanisms of synaptic plasticity
In many regions of the brain, neurons are found to exhibit bidirectional plasticity in which the strength of a synapse can increase or decrease depending on the stimulus protocol; modifiable synapses are generally believed to be the cellular substrate of learning and memory. There is growing experimental evidence that a major component of the postsynaptic expression of plasticity is the regulation of protein receptor trafficking, which results in changes in receptor number at the postsynaptic membrane, and hence modifications in synaptic strength. The total number of synaptic receptors is determined by a non-equilibrium steady state, in which the diffusive flux of surface receptors between synaptic and extrasynaptic domains is balanced by the rate of exchange of receptors with intracellular recycling pools. We are developing mathematical models of these dynamical processes in order to determine the time-dependent distribution of receptors and other proteins across a neuron's synapses and how such distributions are modified during activity-dependent synaptic plasticity. Such models need to take into account intrinsic noise fluctuations arising from the fact that the numbers of synaptic receptors and other proteins are relatively small. One particular focus of our work is to investigate mechanisms of synaptic stabilization, that is, how changes in synaptic strength can persist for days, weeks and even lifetimes in spite of the rapid turnover of synaptic proteins. It is has been hypothesized that synaptic stabilization may involve a coupling between protein receptors and actin polymerization, which is itself regulated by local protein synthesis. The actin cytoskeleton determines synaptic morphology, and the shape/size of a synapse could provide a stable substrate for maintaining changes in synaptic strength. We are also interested in how cellular processes at the synaptic level influence information processing and adaptation at the network level.
| B. A. Earnshaw and P. C. Bressloff. A diffusion-activation model of CaMKII translocation waves in dendrites. J. Comput. Neurosci. 28 77-89 (2010). |
| P. C. Bressloff. Cable theory of protein receptor trafficking in dendritic trees. Phys. Rev. E. 79 041904 (2009). |
| B. A. Earnshaw and P. C. Bressloff. A dynamical corral model of protein trafficking in spines. Biophys. J. 96 1786-1802 (2009). |
| B. A. Earnshaw and P. C. Bressloff. Modeling the role of lateral membrane diffusion in AMPA receptor trafficking along a spiny dendrite. J. Comput. Neurosci. 25 366-389 (2008). pdf |
| P. C. Bressloff, B. A. Earnshaw and M. J. Ward. Diffusion of protein receptors on a cylindrical dendritic membrane with partially absorbing traps. SIAM J. Appl. Math. 68 1223-1246 (2008). pdf |
| P. C. Bressloff and B. A. Earnshaw. Diffusion-trapping model of receptor trafficking in dendrites. Phys. Rev. E 75: 041916 (2007) |
| B. A. Earnshaw and P. C. Bressloff, A biophysical model of AMPA receptor trafficking and its regulation during LTP/LTD. J. Neurosci. 26 12362-12373 (2006). pdf |
Stochastic models of motor-assisted transport in neurons
Although many proteins destined for synapses are conveyed from the cell body, a subset of mRNAs are transported into dendrites to support local protein synthesis. Increasing evidence indicates that local protein synthesis in dendrites plays a critical role in mediating the enduring changes in synaptic structure and function that underlie long-term memory. Within dendrites mRNA is assembled into granules, which then undergo rapid bidirectional transport via multiple molecular motors such as kinesin and dynein. The rapid transport is interspersed with periods of slow movement or pauses, consistent with localization at synaptic sites. We are currently developing stochastic models of motor-driven transport of mRNA granules along dendrites that combines intermittent bidirectional transport with signaling and uptake from targeted synaptic sites. Coupling the transport model with synaptic signaling cascades provides a framework for studying the role of local protein synthesis in long-term plasticity. Moreover, various types of dysfunction in motor-driven transport appear to be a major contributory factor to a number of neurodegenerative diseases associated with memory loss including Alzheimer's.
| J. Newby and P. C. Bressloff. Local synaptic signaling enhances the stochastic transport of motor-driven cargo in neurons. Phys. Biol. 7 036004 (2010). |
| J. Newby and P. C. Bressloff. Random intermittent search and the tug-of-war model of motor-driven transport. J. Stat. Mech P04014 (2010) |
| J. Newby and P. C. Bressloff. Quasi-steady state reduction of molecular-based models of directed intermittent search. Bull. Math. Biol. 72 1840-1866 (2010) |
| J. Newby and P. C. Bressloff. Directed intermittent search for a hidden target on a dendritic tree. Phys. Rev. E 80 021913 (2009). |
| P. C. Bressloff and J. Newby. Intermittent search strategies for delivering mRNA particles to synaptic targets. New J. Phys. 11 023033 (2009). |
| P. C. Bressloff. A stochastic model of NMDA receptor trafficking during synaptogenesis Phys. Rev. E 74 031910 (2006). pdf |
| P. C. Bressloff. A stochastic model intraflagellar trannsport Phys. Rev. E 73 061916 (2006). pdf |
Stochastic neurodynamics
It is well known that the spike trains of individual cortical neurons in vivo tend to be very noisy, having interspike interval (ISI) distributions that are close to Poisson. However, it is far less clear how noise at the single cell level translates into noise at the population level. Nevertheless, it is likely that noise plays an important role in the generation of spontaneous population activity both in vivo and in vitro. Moreover, there is growing evidence that noise can actually be useful, for example, increasing the dynamical range over which coherent oscillations can occur (coherent resonance), enhancing signal detection (stochastic resonance), and the level of noise can act as a tuning parameter for critical dynamics. We are currently developing a master equation formulation of stochastic neural dynamics, which reduces to standard rate-based models in the mean-field limit. Various techniques adapted from the study of biochemical networks can be used to calculate corrections to mean-field theory that take into account higher-order statistics, to calculate escape times from metastable states, and to determine how noise amplifies network oscillations. We are also considering a variety of problems in neuroscience where noise is thought to play a role. One example is the generation of retinal waves during early development, where the statistical nature of spontaneous activity plays an important role in the activity-dependent development of visual cortex. Another example is the role of noise in generating rhythmic burst oscillations in a recurrently connected network of neurons possessing slow activity-dependent depression or adaptation. Such rhythms have been found in several brain areas including the Pre-Botzinger complex (PreBotC) and the developing chick spinal cord.
| P. C. Bressloff. Metastable states and quasicycles in a stochastic Wilson-Cowan model of neural population dynamics. Phys. Rev. E 82 051903 (2010) |
| P. C. Bressloff. Stochastic neural field theory and the system-size expansion. SIAM J. Appl. Math 70 1488-1521 (2009) |
| W. H. Nesse, C. Del Negro and P. C. Bressloff. Oscillation regularity in noise-driven excitable systems with multi-timescale adaptation. Phys. Rev. Lett. 101 088101 (2008) |
| W. H. Nesse, A. Borisyuk and P. C. Bressloff. Fluctuation-driven rhythmogenesis in an excitatory neuronal network with slow adaptation. J. Comput. Neurosci. 25 317-333 (2008). pdf |
Continuum neural field models of large-scale cortical dynamics
Analysis of the dynamical mechanisms underlying the formation of spatially coherent activity states in the brain is crucially important for understanding a wide range of neurobiological phenomena, both naturally occurring and pathological. For example, neurological disorders such as epilepsy and migraine are characterized by travelling waves propagating across the surface of the brain. Spatially coherent activity states are also prevalent during the normal functioning of the brain, encoding local properties of visual and auditory stimuli, encoding head direction and spatial location, and maintaining persistent activity states in short-term working memory. Continuum neural field models represent the large-scale dynamics of populations of neurons in terms of nonlinear integrodifferential equations whose associated integral kernels represent the spatial distribution of neuronal synaptic connections at multiple spatial scales. As in the case of nonlinear PDE models of diffusively coupled excitable systems, neural field models can exhibit a variety of coherent structures including both stationary and travelling pulses, spatially periodic patterns, and spatially localised oscillations. We are interested in analysing the existence and stability of these coherent structures, and exploring their role in cortical processing, higher cognitive processing such as working memory, and various neuropathologies.

| Z. Kilpatrick and P. C. Bressloff. Stability of bumps in piecewise smooth neural fields with nonlinear adaptation. Physica D 239 1048-1060 (2010). |
| Z. Kilpatrick and P. C. Bressloff. Effects of synaptic depression and adaptation on spatiotemporal dynamics of an excitatory neuronal network. Physica D 239 547-560 (2010). |
| Z. Kilpatrick and P. C. Bressloff. Spatially structured oscillations in a 2D excitatory neuronal network with synaptic depression J. Comput. Neurosci. 28 193-209 (2010). |
| Z. Kilpatrick, S. E. Folias and P. C. Bressloff. Traveling pulses and wave propagation failure in an inhomogeneous neural network. SIAM J. Appl. Dyn. Syst. 7 161-185 (2008). pdf |
| S. E. Folias and P. C. Bressloff, Breathers in two-dimensional excitable neural media. Phys. Rev. Lett. (2005). pdf |
| P. C. Bressloff, Weakly interacting pulses in synaptically coupled neural media. SIAM J. Appl. Math. 66: 57-81(2005). pdf |
| S. E. Folias and P. C. Bressloff, Stimulus-locked traveling waves and breathers in an excitatory neural network. SIAM J. Appl. Math. 65:2067-2092 (2005). pdf |
| S. E. Folias and P. C. Bressloff, Breathing pulses in an excitatory neural network. SIAM J. Appl. Dyn. Syst. 3:378-407 (2004). pdf |
| P. C. Bressloff and S. E. Folias, Front bifurcations in an excitatory neural network. SIAM J. Appl. Math. 65:131-151 (2004). pdf |
| P. C. Bressloff, S. E. Folias, A. Pratt and Y-X Li, Oscillatory waves in inhomogeneous neural media. Phys. Rev. Lett. 91:178101 (2003). pdf |
| P. C. Bressloff, Traveling fronts and wave propagation failure in an inhomogeneous neural network Physica D 155 :83-100 (2001). pdf |
Recurrent network models of primary visual cortex (V1)
The responses of neurons in sensory cortices are affected by the spatial context within which stimuli are embedded. In primary visual cortex (V1), orientation-selective responses to stimuli in the receptive field (RF) center are suppressed by similarly oriented stimuli in the RF surround. Suppression from the RF surround, which may represent the neural correlate of perceptual figure-ground segregation, is traditionally thought to be generated within V1 via horizontal connections. Recently, it has been shown that these connections are too short and slow to mediate fast suppression from distant regions of the RF surround. In collaboration with Alessandra Angeluci (Moran Eye Center), we have developed a recurrent network model of V1 in order to show how feedback connections, which are faster and longer range than horizontal connections, can generate far surround suppression. Our model provides a solution to how suppression can arise from excitatory feedback contacting predominantly excitatory neurons. It also makes the novel prediction that the "suppressive far surround" is not always suppressive, and this has recently been verified experimentally. We are currently working on an extension of the model that explicitly incorporates orientation tuning and selectivity, in order to investigate the mechanisms underlying orientation-specific center-surround interactions in V1. Our basic approach will be to incorporate feedback into a coupled hypercolumn model. The internal structure of each hypercolumn is idealized as a ring of orientation selective cells labeled by their orientation preference leading to the so-called coupled ring model of V1. We are also considering more complicated hypercolumn models that incorporate other feature preferences such as spatial frequency (eg. the spherical model of a hypercolumn). One important component of our work concerns the different classes of inhibitory interneurons (eg. horizontally projecting basket cells vs. vertically projecting local interneurons) and their role in contextual processing. Yet another aspect of our our work concerns how attentional modulation via feedback influences the responses to contextual stimuli.
| J. Icheda, L. Schwabe, P. C. Bressloff and A. Angelucci. Response facilitation from the ``suppressive'' surround of V1 neurons. J. Neurophysiol. 98 2168-2181 (2007). |
| L. Schwabe, A. Angelucci, K. Obermayer and P. C. Bressloff. The role of feedback in shaping the extra-classical receptive field of cortical neurons: a recurrent network model J. Neurosci. 26 9117-9129 (2006). |
| A. Angelucci and P. C. Bressloff. The contribution of feedforward, lateral and feedback connections to the classical receptive field center and extra-classical receptive field surround of V1 neurons Prog. Brain Res. 154 93-121 (2006). |
| J. S. Lund, A. Angelucci and P. C. Bressloff, Anatomical substrates for the functional column in primary visual cortex. Cerebral Cortex 12:15-24 (2003). pdf |
| P. C. Bressloff and J. D. Cowan, The functional geometry of local and long-range connections in a model of V1. J. Physiol. (Paris) 97: 221-236 (2003). pdf |
| P. C. Bressloff and J. D. Cowan, Spherical model of orientation and spatial frequency tuning in a cortical hypercolumn. Phil. Trans. Roy. Soc. B 358:1643-1667 (2003). pdf |
| P. C. Bressloff and J. D. Cowan, SO(3) symmetry breaking mechanism for orientation and spatial frequency tuning in visual cortex. Phys. Rev. Lett. 88 : 078102 (2002). pdf |
| P. C. Bressloff and J. D. Cowan, An amplitude equation approach to contextual effects in primary visual cortex Neural Comput. 14 :493-525 (2002). pdf |
Cortical development
We are studying a variety of activity-based models for the development of the functional architecture of primary visual cortex. For example, we have recently constructed an activity-based developmental model of ocular dominance (OD) column formation in primary visual cortex that takes into account cortical growth. The resulting evolution equation for the densities of feedforward afferents from the two eyes exhibits a sequence of pattern forming instabilities as the size of the cortex increases, such that the mean width of an OD column is approximately preserved during the course of development. This is consistent with recent experimental observations of postnatal growth in cat. We are also investigating activity-based models for the joint development of OD columns and CO blobs that take into account the laminar structure of cortex. In yet other work we have extend the theory of self-organizing neural fields in order to analyze the joint emergence of topography and feature selectivity in primary visual cortex through spontaneous symmetry breaking. In particular we have shown how a two-dimensional isotropic topographic map can undergo a pattern forming instability that breaks the underlying rotation symmetry. This leads to the formation of elongated activity bumps consistent with the emergence of orientation preference columns. A particularly interesting property of the latter symmetry breaking mechanism is that the linear equations describing the growth of the orientation columns exhibits a rotational shift-twist symmetry, in which there is a coupling between orientation and topography.
| P. C. Bressloff and A. M. Oster, A theory for the alignment of cortical feature maps during development. Phys. Rev. E 82 021920 (2010). pdf |
| A. M. Oster and P. C. Bressloff, A developmental model of ocular dominance formation on a growing cortex Bull. Math. Biol. 68 73-98 (2006). pdf |
| P. C. Bressloff, Spontaneous symmetry breaking in self-organizing neural fields Biol. Cybern. 93: 256-274 (2005). pdf |
Geometric visual hallucinations and Euclidean shift-twist symmetry
In collaboration with Jack Cowan (University of Chicago) and Marty Golubitsky (University of Houston), we have developed a theory of geometric visual hallucinations based on the original idea of Ermentrout and Cowan that some disturbance such as a drug or flickering light can destabilize the visual part of the brain inducing a spontaneous pattern of cortical activity. The geometry of the resulting hallucination thus reflects the intrinsic architecture of the visual cortex. Our work has focused on a continuum model of V1 in which cells signal both the position and orientation of a local stimulus. Using symmetric bifurcation theory, we have shown that the cortical activity patterns underlying common visual hallucinations can be accounted for in terms of certain symmetry properties of the lateral connections, specifically, that they are invariant under the action of the planar Euclidean group - the group of rigid motions in the plane - rotations, reflections and translations. The resulting representation is twisted due to an anisotropy in the lateral connections, which tends to favor directions that are correlated with the orientation preferences of the interacting cells. More recently we have shown how spatially periodic correlations between the pattern of synaptic connections within V1 and cortical feature maps can induce a pinning of spontaneous activity patterns to the underlying feature maps. We have also been considering the role of Euclidean shift-twist symmetry in other areas of biology. For example, a wide variety of self-organizing biological systems exhibit aggregation and alignment phenomena. These occur spontaneously due to mutual interactions between the individual elements of a population, in which both the relative position and the relative orientation of the individuals has a significant effect on the nature of the interactions. Examples include the alignment of actin filaments within a cell's cytoskeleton, the alignment of mammalian fibroblast cells within the extracellular matrix, and the aggregation of animal social groups. We have shown how the aggregation and alignment of oriented objects in two dimensions can be modeled in terms of non-local population models, in which the underlying interaction kernel is invariant under the shift-twist action of the Euclidean group previously studied within the context of our continuum model of primary visual cortex.
| P. C. Bressloff and Z. Kilpatrick, A nonlocal Ginzburg-Landau equation for cortical dynamics. Phys. Rev. E 78 041916 (2008) |
| P. C. Bressloff, Euclidean shift-twist symmetry in population models of self-aligning objects. SIAM J. Appl. Math. 64: 1668-1690 (2004). pdf |
| P. C. Bressloff, Pattern formation in visual cortex. Les Houches Lectures in Neurophysics (2004). ps |
| P. C. Bressloff, Bloch waves, periodic feature maps and cortical pattern formation. Phys. Rev. Lett. 89 : 088101 (2002). pdf |
| P. C. Bressloff, Spatially periodic modulation of cortical patterns by long-range horizontal connections. Physica D 185:131-157 (2003). pdf |
| P. C. Bressloff, J. D. Cowan, M. Golubitsky, P. J. Thomas and M. Wiener, What geometric visual hallucinations tell us about the visual cortex Neural Comput. 14 : 473-491 (2002). pdf |
| P. C. Bressloff, J. D. Cowan, M. Golubitsky and P. J. Thomas, Scalar and pseudoscalar bifurcations motivated by pattern formation on the visual cortex. Nonlinearity 14 :739-775 (2001). |
| P. C. Bressloff, J. D. Cowan, M. Golubitsky, P. J. Thomas and M. Wiener, Geometric visual hallucinations, Euclidean symmetry and the functional architecture of striate cortex Phil. Trans. Roy. Soc. B 40 :299-330 (2001). pdf |
Spiking neuron models
The dynamics of coupled oscillator arrays has been the subject of much recent experimental and theoretical interest. Example systems include Josephson junctions, lasers, oscillatory chemical reactions, heart pacemaker cells, central pattern generators and cortical neural oscillators. Most work in this area has been concerned with smoothly coupled oscillators under the assumption of weak interactions so that averaging methods can be used to reduce the system to a phase model. On the other hand, many oscillators in nature communicate via pulses. Examples include neural oscillators, fireflies, digital phase-locked loops and certain models of self-organized criticality. In collaboration with Steve Coombes (University of Nottingham), we have developed a theory of strong coupling instabilities in networks of integrate-and-fire (IF) neurons. An IF neuron fires a spike whenever its state variable reaches some threshold, and immediately after firing the state variable is reset to some zero resting level - the dynamics can thus be reduced to a nonlinear mapping of the firing times (threshold-crossing times) of the neurons. For sufficiently slow synaptic interactions the network behaviour is compatible with a corresponding firing rate model obtained by performing a short-term time-average of the IF dynamics. Our theory has been applied to a number of neural systems including swimming locomotion in Xenopus, orientation tuning in primary visual cortex, and wave propagation in excitable neural tissue. In related work, we have developed an integrate-and-fire model of propagating saltatory waves in active dendritic spines.
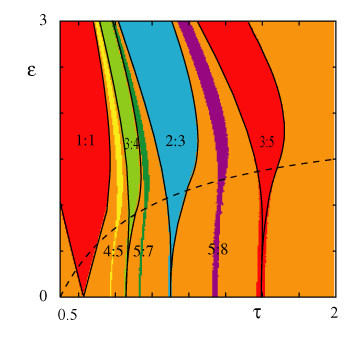
| S. Coombes and P. C. Bressloff, Saltatory waves in the spike-diffuse-spike model of active dendrites. Phys. Rev. Lett. 91:028102 (2003). pdf |
| P. C. Bressloff, Traveling waves and pulses in a one-dimensional network of integrate-and-fire neurons. J. Math. Biol. 40 :169-183 (2000). pdf |
| S. Coombes and P. C. Bressloff, Solitary waves in a model of dendritic cable with active spines. SIAM J. Appl. Math. 61:432-453 (2000). pdf |
| P. C. Bressloff and S. Coombes, Dynamical theory of spike train dynamics in networks of integrate-and-fire oscillators. SIAM J. Appl. Math. 60:828-841 (2000). pdf |
| P. C. Bressloff and S. Coombes, Dynamics of strongly coupled spiking neurons. Neural Comput. 12 :91-129 (2000). pdf |
| P. C. Bressloff and S. Coombes, Travelling waves in a chain of pulse-coupled integrate-and-fire oscillators with distributed delays. Physica D 130:232-254 (1999). pdf |
| P. C. Bressloff, Mean-field theory of globally coupled integrate-and-fire neural oscillators with dynamic synapses. Phys. Rev. E 60:2180-2190 (1999). |
| S. Coombes and P. C. Bressloff, Mode-locking and Arnold tongues in integrate-and-fire neural oscillators. Phys. Rev. E 60:2086-2096 (1999). |
| P. C. Bressloff and S. Coombes, Travelling waves in chain of pulse-coupled oscillators. Phys. Rev. Lett. 80:4815-4818 (1998). pdf |
| P. C. Bressloff and S. Coombes, Desynchronization, mode-locking and bursting in strongly-coupled integrate-and-fire oscillators. Phys. Rev. Lett. 81:2168-2171 (1998). pdf |
| P. C. Bressloff and S. Coombes, Spike train dynamics underlying pattern formation in an integrate-and-fire oscillator network. Phys. Rev. Lett. 81:2384-2387 (1998). pdf |
For more information contact Paul C. Bressloff, 5-1633