Morse theory

Suppose f is a continuously differentiable function of 2 real variables x,y satisfying

f(x+1,y)=f(x,y+1)=f(x,y).


Then there are at least 3 distinct pairs of numbers x,y in the interval [0,1) so that both partial derivatives of f are 0 at these points (i.e. (x,y) are critical points).

The displayed equation guarantees that f is determined by its values on the unit square [0,1]x[0,1] , and further the values on the opposite sides of the square coincide. So it is natural to identify (or glue together) the opposite sides to obtain a torus (popular science literature refers to it as a ``donut''). The point is that f is really defined on the torus. There is an extremely useful method, called Morse theory, that relates the structure of a space (e.g. the torus) and the structure of the set of critical points. Try constructing a function f as above that has exactly 3 critical points.


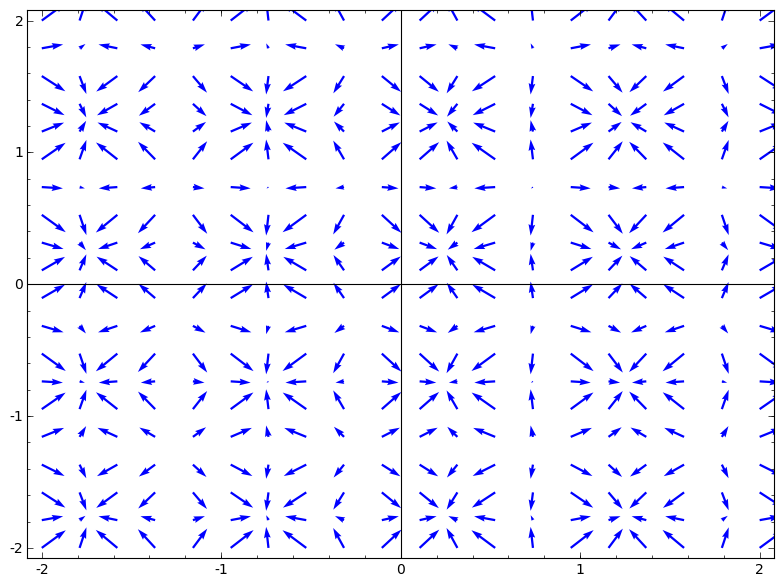
gradient flow

This is the picture of the gradient vector field of the function f(x,y)=sin(2Àx)+sin(2Ày). Observe sources, sinks, and saddle points.