The Commutation Problem
The purpose of this page is to organize results of some
experiments I ran regarding the infamous
commutation problem
in multivariate splines, including some color pictures that
are hard to handle or publish otherwise.
The underlying triangulation in all cases consists of four
triangles all sharing one interior vertex.
The results are summarized in the table
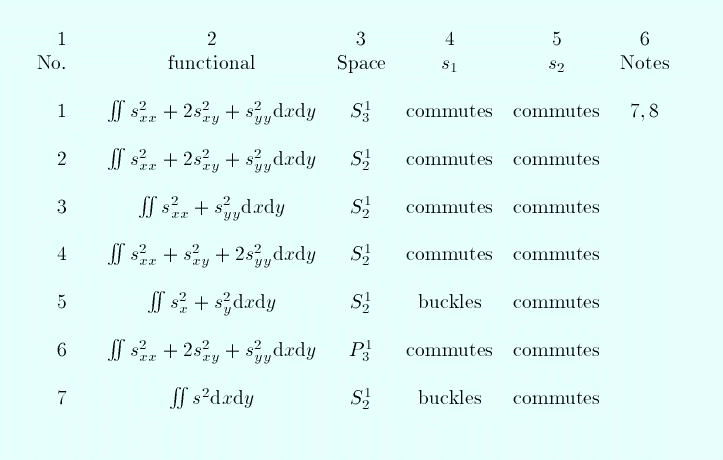
The individual spaces are:
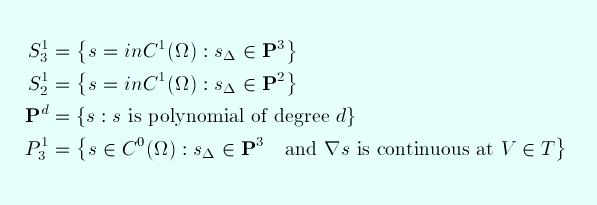
Parts of the notation, and the term commutes, are
defined in a
technical description
of the commutation problem. The term buckles means
that the diagram does not commute.
Notes
-
Column 1 gives the reference number of the example.
-
Column 2 gives the functional that is being minimized
(subject to interpolation). The integration is over the
domain Omega, which is the union of the triangles. The
triangulation consists of one interior vertex shared by
four triangles having vertices (1,1),
(-1,1), (-1,-1), (1,-1). The
interior vertex is allowed to vary in Omega. When it is
at the origin we have a singular vertex where
the dimension of the space of differentiable piecewise
cubics or quadratics increases by 1 (from 15 to 16 for
cubics and from 7 to 8 for quadratics).
-
Column 3 gives the function space over which the
functional is minimized. The space in example 6 is the
space of continuous piecewise cubic functions that are
differentiable at the vertices of the traingulation, but
not in the interior of the edges shared by triangles.
-
Column 4 gives the behavior of the interpolant for the
cardinal function at V1, i.e., the function
that's 1 at V1 and 0 at the other four
vertices.
-
Column 5 similarly describes the behavior for the
cardinal function associated with the interior vertex.
-
Column 6 refers to notes explained in this list.
-
This is the most frequently considered situation. From
a likelyhood point of view
it is amazing that the diagram commutes.
-
Remarkably, the solution for the interior vertex being
in singular position turns out to be a single quadratic
function, namely:
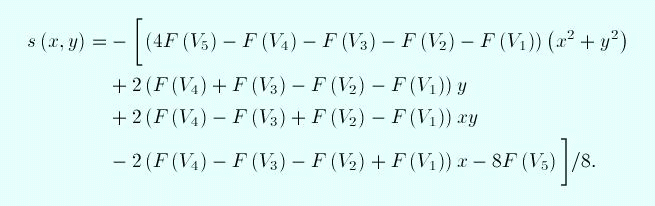 As yet I am unable to compute the solution explicitly
for a general non-singular vertex - instead the code
solves an appropriate linear system that depends on the
location of the interior vertex. It is remarkable that
the solution at singularity is the same for all
variation principles in examples 1, 2, and 3. The
corresponding statement does not hold for non-singular
vertices.
As yet I am unable to compute the solution explicitly
for a general non-singular vertex - instead the code
solves an appropriate linear system that depends on the
location of the interior vertex. It is remarkable that
the solution at singularity is the same for all
variation principles in examples 1, 2, and 3. The
corresponding statement does not hold for non-singular
vertices.
-
You may see
pictures
of this example.
[17-Jul-1996]
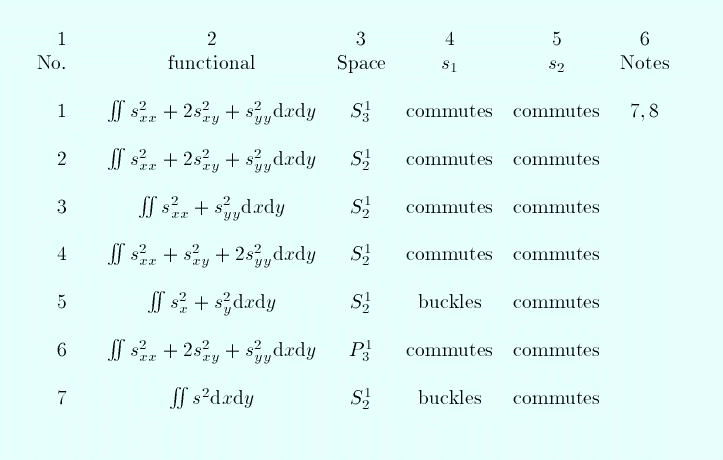
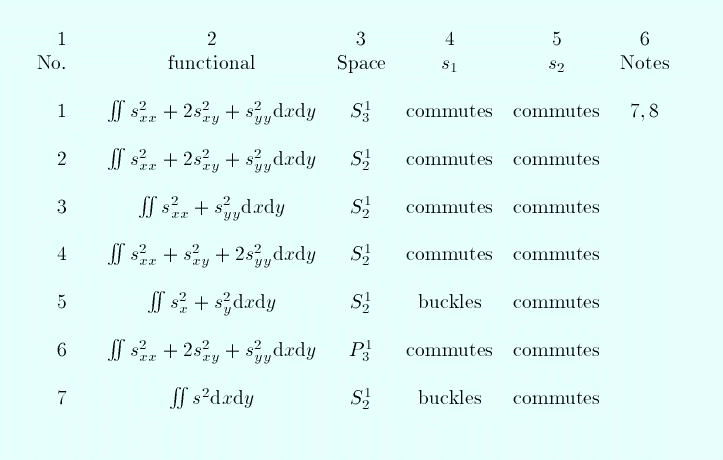
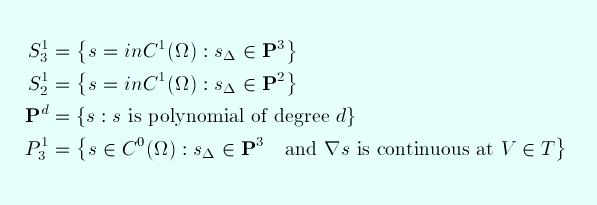
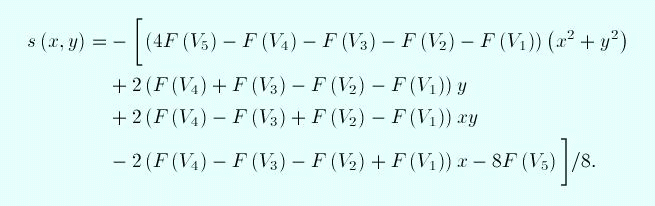 As yet I am unable to compute the solution explicitly
for a general non-singular vertex - instead the code
solves an appropriate linear system that depends on the
location of the interior vertex. It is remarkable that
the solution at singularity is the same for all
variation principles in examples 1, 2, and 3. The
corresponding statement does not hold for non-singular
vertices.
As yet I am unable to compute the solution explicitly
for a general non-singular vertex - instead the code
solves an appropriate linear system that depends on the
location of the interior vertex. It is remarkable that
the solution at singularity is the same for all
variation principles in examples 1, 2, and 3. The
corresponding statement does not hold for non-singular
vertices.