








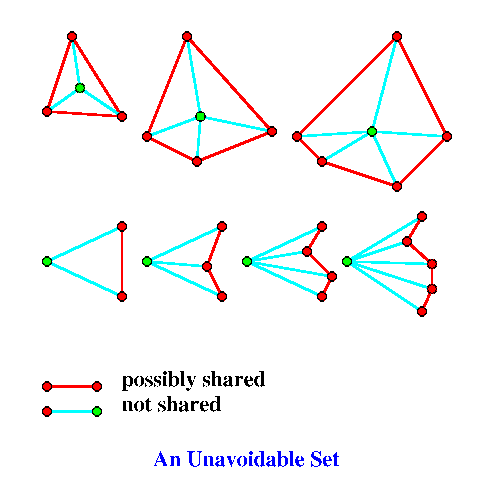
The vertex whose star we consider is marked green. Red edges may be shared with the rest of the triangulation. Thus the first three configurations are the stars of interior vertices of degree 3, 4, or 5. The remaining configurations may arise as the stars of boundary vertices of degree 2, 3, 4, or 5.
However, in the proof of the dimension statement for S14 we
consider subtriangulation, and so the first three
configurations in the second row may also arise as
subtriangulations of the star of an interior vertex, part of
which has already been removed.
[01-Nov-2023]