








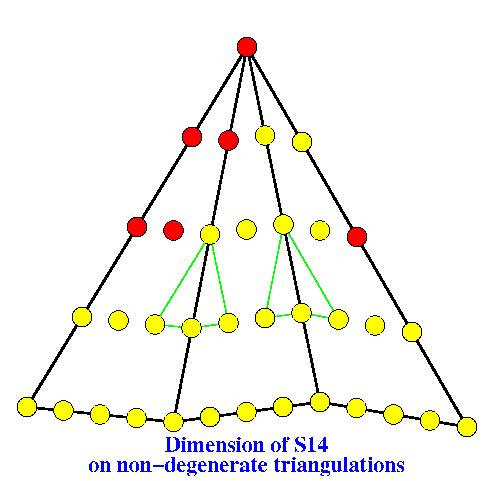
This proof clearly demonstrates the power of the Bernstein Bézier form. We will be able to show that the dimension of S14 (on non-degenerate triangulations) equals 6V-3.
The proof is by induction. The statement is clearly true for a single triangle where V=3 and 6V-3=15 . Note that a bivariate quartic polynomial has 15 degrees of freedom.
For the induction step consider a boundary vertex v of the triangulation and all triangles sharing v. In the picture above, v is the vertex marked with a red dot at the very top. Let U be the star of v , i.e., the set of triangles containing the vertex v. Removing U the triangulation. We must show that this operations decreases the dimension of the spline space by 6. Alternatively, adding the vertex v should increase the dimension by 6.
Let T be the triangulation obtained by removing v and its attached triangles. Observe that every spline on T can be extended into U. This is illustrated in the figure above, where U shares the bottom three edges with T. The continuity and differentiability conditions determine the first two rows of of Bézier ordinates marked in yellow. The differentiability conditions marked by the green quadrilaterals imply two more of the points marked in yellow.
Next we assign arbitrary values to the Bézier ordinates whose domain points are marked red. These in turn determine the remaining Bézier ordinates marked yellow. Since we have six points marked red the dimension does indeed increase by six.
This page is a somewhat casual description that's meant to illustrate the essential techniques. Strictly speaking, our argument gives only an upper bound on the dimension of S14 since we show that setting 6V-3 Bézier ordinates implies values for all other Bézier ordinates. A more rigorous proof requires either the combination of the statement here with a lower bound or the construction of cardinal functions.
For a more rigorous statement see the proof of Theorem 1 in
Peter Alfeld, Bruce Piper, and L.L. Schumaker, An Explicit Basis for C 1 Quartic Bivariate Splines, SIAM J. Num. Anal. 24 (1987), pp. 891-911.
[01-Nov-2023]