Department of Mathematics, University of Utah
	Department of Mathematics, College of Science, University of Utah, Salt Lake City, Utah 84112-0090, USA. 801-581-6851, 801-581-4148 (fax)

A more detailed discussion of reducibility.

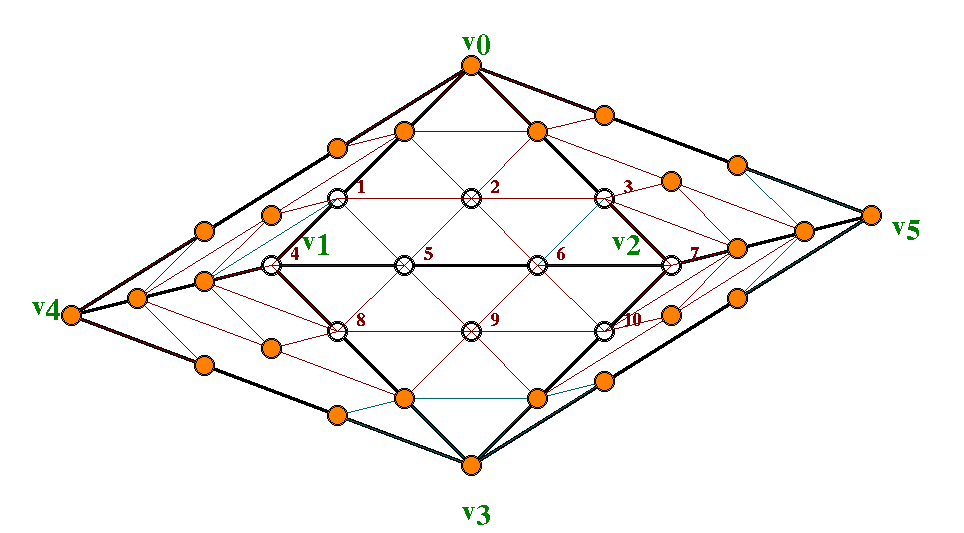
Let us consider the edge configuration e44 in more detail, as indicated in the nearby figure.

The dimension of S13 on that configuration is

To embed the configuration into a triangulation we need to impose 16 conditions on the boundary of e44. Thus we should be left with one free parameter. To see that this is indeed so we need to analyze a system of smoothness conditions. Let's label the vertices as indicated by v ₀, v ₁, v ₂, v ₃, v ₄, v ₅ in the Figure, and the unknowns as c _i where the subscripts are given in dark red type in the figure. We describe the geometry of the configuration in terms of barycentric coordinates as follows:

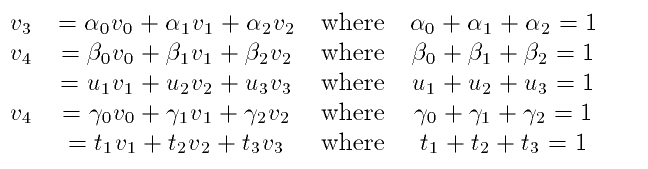
Suppose now that a spline is specified on the outside of e44. That means that the Béezier ordinates corresponding to domain points marked in gold are determined by the smoothness conditions. Let us suppose they are all zero. There must be a space of dimension 2 of splines on e44 that satisfy these homogeneous boundary conditions. The available Béezier (marked as black circles with white interiors must satisfy the smoothness equations:

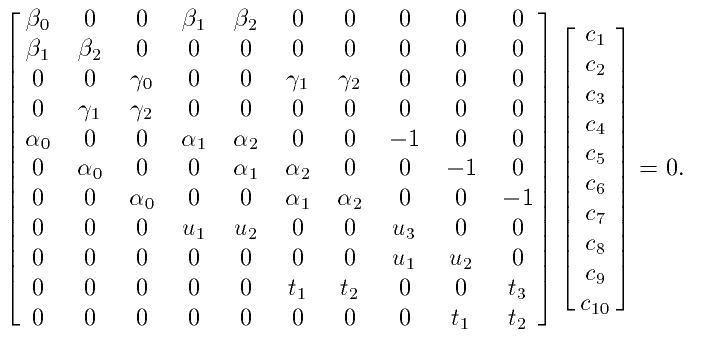
This is a homogeneous system of eleven equations in 10 unknowns that is supposed to have a one dimensional solution space. Thus the rank of the matrix should be nine. To see this we need to identify a nine by nine submatrix that is non-singular. For example, if we omit the first two rows and the first column we obtain (using symbol manipulation) the determinant

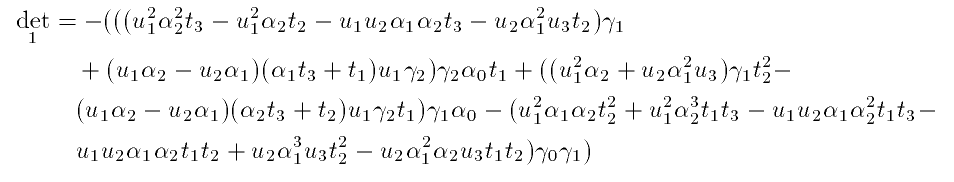
However, the barycentric coordinates of the various points with respect to the various triangles are not independent. Using the substitution

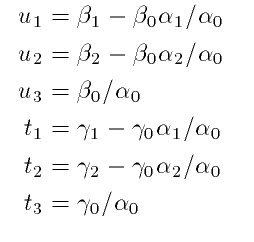
we find out that this determinant is actually zero. (The reason for including this example is to illustrate that the determinant of a submatrix may be zero in a non-obvious way.) However, if we omit instead the first and the third row, as well as the first column, we obtain

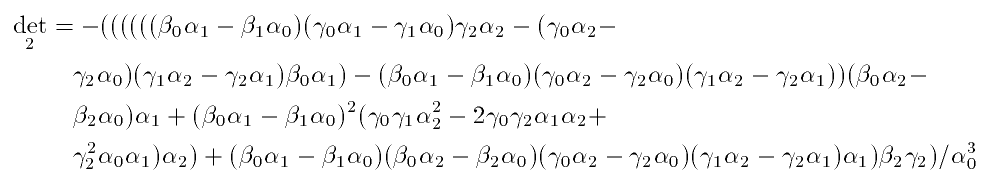
We now have to show that this determinant is non-zero. We may use some properties of the barycentric coordinates, e.g.,

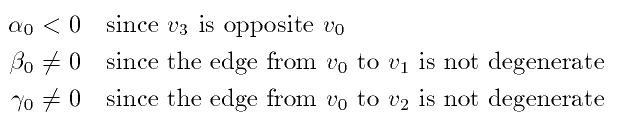
This seems to be a formidable task. I've looked at all possibilities of omitting two rows and one column, and none of these possibilities seems to lead to an expression that's simple. However, I would expect that given sufficient motivation this problem is tractable.