
Why Logarithms?
It turns out that the only (non-zero differentiable) functions with the
key property
are logarithmic
functions. To see this we derive a differential equation for 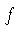 whose solution is a logarithm. Differentiating in
whose solution is a logarithm. Differentiating in 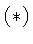 with
respect to
with
respect to 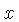 gives
Similarly, differentiating with respect to
gives
Similarly, differentiating with respect to 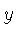 gives
Hence
In the special case
gives
Hence
In the special case 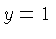 this turns into
From
this turns into
From 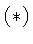 if follows that
if follows that 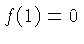 . The solution of this
initial value problem is
where
. The solution of this
initial value problem is
where 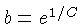 and
and 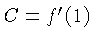 is an arbitrary constant.
is an arbitrary constant.
So only logarithms work. However, if you want to settle for
properties that are more complicated than 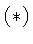 there are other
possibilities. For example, you may want to think about how to
construct a slide rule based on the identity
there are other
possibilities. For example, you may want to think about how to
construct a slide rule based on the identity

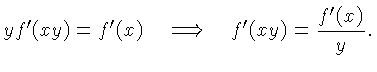

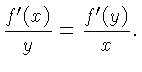
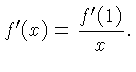
![]() there are other
possibilities. For example, you may want to think about how to
construct a slide rule based on the identity
there are other
possibilities. For example, you may want to think about how to
construct a slide rule based on the identity ![$\displaystyle \sin x \sin y =
\frac{1}{2}[\cos(x-y) - \cos(x+y)].$](img15.gif)