
What Can You Do With A Slide Rule?
There was a time when electronic calculators did not yet exist.
This did not stop us from doing complicated things, like going to the
moon, figuring out the double helix, or designing the Boeing 747. In
those days, when we needed to compute things, we used slide
rules which are marvelous and beautiful instruments!
There are many pages about slide rules on the web, and you can
still buy brand new slide rules (40 years old but never used, and
still in their factory supplied box) in various places. The purpose
of this particular and quite idiosyncratic slide rule page is to
describe common scales used on slide rules, and the kind of
mathematical expressions that could be evaluated with those scales.
A subsidiary of this page describes a software package that let's you enter
an expression and will tell you how that expression can be evaluated with a slide rule. If you are looking for that software go here.

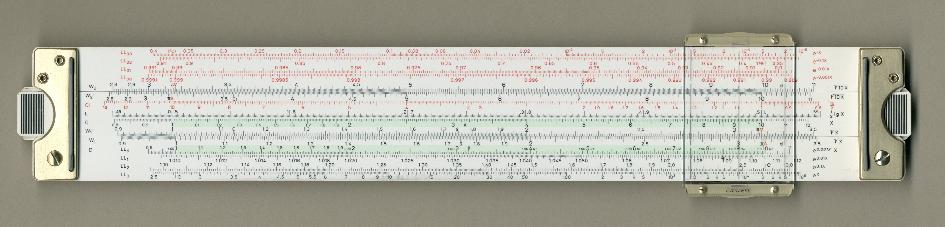
The two images on this page were scanned by Clark McCoy of the
Oughtred Society.
They show the two sides of a particular
slide rule in my collection. This is one of the fanciest and
most beautiful slide rules ever made, a Faber Castell Novo
Biplex 2/83 N. It's made of plastic, and has 30 scales and 11
cursor marks. The rule is about 13.5 inches long and 2.25 inches wide.
You can click on the pictures and see an enlarged image, but that
doesn't come close to holding the real thing in your hands. It feels
heavy and solid. The slide and cursor move with silky smoothness and
yet they stay in place wherever you let go of them. The lettering is
crisp and detailed, and pristine! No space is wasted, but the
information is not crowded either. Every scale has a purpose.
German made slide rules of that time (the late 1960s) usually come
with an accessory plastic ruler. This particular slide rule has a
ruler (not shown) that lists common formulas and physical data on one
side. Those may be useful for slide rule calculations. However, the
other side of that ruler has a detailed list and explanation of common
notations in set theory! This is about as useless for slide
rule calculations as a list of large mammals. Apparently this slide
rule was made when the "new math" was at its zenith and Faber Castell
wanted its share of the action.
The Basic Idea
It's clear how to add or subtract two lengths using two ordinary
rulers. Slide rules do the same thing, add and subtract lengths, but
they don't call them lengths. For example, by calling them
logarithms, you can multiply and divide numbers. In fact, I don't
know of any slide rule that actually let's you add or subtract
numbers. In the heyday of slide rules that was considered a trivial
task that you did in your head, or on a piece of paper if you had to.
[Jeff Weiner brought to my attention that actually there are some
slide rules that can add and subtract, specifically the Pickett
Microline 115 and the Pickett 901 rules.]
A slide rule consists of three parts: the body, the
slide, and the cursor. The body and the slide are marked
with scales. The cursor has a hairline that facilitates accurate
positioning of the cursor at a specific point on some scale. There
may be other marks on the cursor that are used for specific and
special purposes.
Basic Multiplication
The most basic procedure carried out on a slide rule is the
multiplication of two numbers u and v using the C
and D scales. These two scales are identical. C is on
the slide, and D is on the body. Move the hairline over
u on the D scale. Move the slide so that its beginning
(marked by
1 on the C scale, and also called the index of
the C scale) lines up with the hairline. Move the hairline to
the number v on the C scale. Read the result underneath
the hairline on the
D scale. If the number v projects beyond the end of the
slide rule move the end of the slide rule (marked with 10 on
the C scale) above u and read the result as before on
the D scale underneath the number v on the C
scale.
Why?
Why does this work? The C and D scales show a number
x that equals the exponential of the distance of x from
the beginning of the C or D scale. So basically you are
adding the logarithms of the numbers u and v, and the
logarithm of the product equals the sum of the logarithms. This is
the fundamental identity underlying all slide rule calculations, and
it is worth stating prominently:
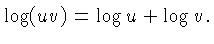
It's convenient to think of the logarithm as the common (base 10)
logarithm, and the length of the slide rule as one unit, but you can
also think of log meaning the natural logarithm, and the length
of the slide rule being log(10) units.
The multiplication of two numbers exhibits two important
properties of slide rule calculations:
- The real number line is infinite and slide rules have finite
length. Hence all scales can only show a part of the real number
line. On the C and D scales, any number x is
shown as a number between 1 and 10, and it is determined only up to a
factor that is an integer power of 10. In other words your
slide rule does not usually show the location of the decimal point.
You are supposed to understand your problem well enough so you can
tell where to put it. The slide rule also does not tell you the sign
of your result.
- Compared to a calculator, a slide rule is severely limited in
its accuracy. You can enter and read a number typically to two or
three decimal digits only.
Scales
All other scales on a slide rule are referenced to the C
and D scales. Following is a list of scales commonly found on
slide rules. For each scale we list the name (like C), the
function underlying it (like  ), and some explanations or comments.
), and some explanations or comments.
| Name |
function |
Comments |
|
| C, D | 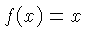 | The basic scales. C is on the slide,
D on the body.
|
| CI, DI | 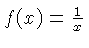 | CI is on the slide,
DI on the body.
|
| CF, DF | 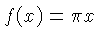 | CF is on the slide,
DF on the body.
|
| CIF, DIF | 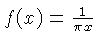 | CIF is on the slide,
DIF on the body.
|
| A, B | 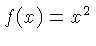 | A is on the body,
B is
on the slide.
|
| R, W | 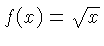 | May come with subscripts to
distinguish 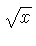 and and 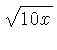 , and have a prime
attached to distinguish location on the body or slide.
These scales are labeled R
(Root) or W
(Wurzel). The radical symbol may also be used. , and have a prime
attached to distinguish location on the body or slide.
These scales are labeled R
(Root) or W
(Wurzel). The radical symbol may also be used.
|
| K | 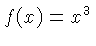 |
This scale usually occurs by itself, rather than as a member of a pair.
|
| LL, E | 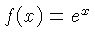 or or 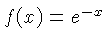 | This is one of
the scales that show the decimal point. Usually there are several
scales, like
and
.
|
| L | 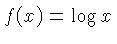 | The only scale on a slide rule that
has a constant increment. Usually on the slide. If there was one such
scale on the slide and one on the body they could be used for the
addition
of numbers.
|
| S | 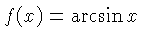 , , 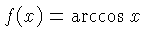 | Lists the
angle 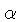 for which for which 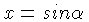 of of 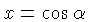 .
On slide rules, all angles are measured in degrees, and reside in the interval .
On slide rules, all angles are measured in degrees, and reside in the interval
![$ [0^\circ,90^\circ]$](qimg20.gif) . The scale usually lists both . The scale usually lists both
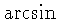 and and 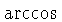 , using the identity , using the identity
|
| T | 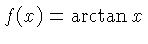 , , 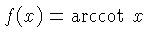 | Similar to
the S scale. 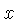 is in the interval is in the interval ![$ [0.1,1]$](qimg27.gif) , , 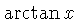 is in
is in![$ [5.8^\circ,45^\circ]$](qimg29.gif) and and 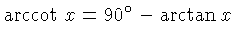 . There may be a similar scale of . There may be a similar scale of 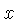 in the interval in the interval
![$ [1,10]$](qimg31.gif) in which case subscripts may be used to distinguish the
scales. in which case subscripts may be used to distinguish the
scales.
|
| ST | 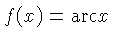 | showing the angle (in
degrees) in the unit circle for an arc of length 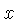 where where 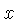 is
in the interval is
in the interval ![$ [0.01,0.1]$](qimg33.gif) . For such small arcs, within the
accuracy of a slide rule, the angle (measured in radians), the sine,
and the tangent are all equal. . For such small arcs, within the
accuracy of a slide rule, the angle (measured in radians), the sine,
and the tangent are all equal.
|
| P | 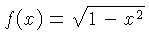 | for 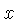 in the interval in the interval
![$ [0.1,1]$](qimg27.gif) . The Pythagorean Scale. . The Pythagorean Scale.
|
| H | 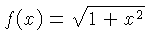 | for 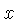 in the interval in the interval
![$ [0.1,1]$](qimg27.gif) . There may be another scale for . There may be another scale for 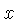 in in ![$ [1,10]$](qimg31.gif) and the two scales may be distinguished by subscripts.
and the two scales may be distinguished by subscripts.
|
| Sh | 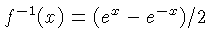 | 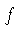 is the inverse of
the hyperbolic sine. is the inverse of
the hyperbolic sine.  is in the interval is in the interval ![$ [1,10]$](qimg31.gif) If a scale
is present for If a scale
is present for  in in ![$ [0.1,10]$](qimg38.gif) the scales may be distinguished
by subscripts. the scales may be distinguished
by subscripts.
|
| Ch | 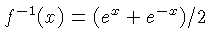 | 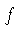 is the
inverse of the hyperbolic cosine. is the
inverse of the hyperbolic cosine. 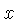 is in the interval is in the interval ![$ [1,10]$](qimg31.gif) . .
|
| Th | 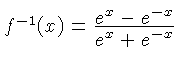 | 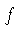 is
the inverse of the hyperbolic tangent. is
the inverse of the hyperbolic tangent. 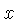 is in the interval is in the interval ![$ [0.1,1]$](qimg27.gif) . .
|
Table 1: Common Scales
One Variable
The power of a slide rule stems from the interplay of the scales and
the movements of the slide and the cursor. However, even if your
slide was lined up with the scales on the body, but otherwise frozen
in place, you could use your slide rule as a lookup table for a large
number of formulas. Some of them are listed in Tables 2 and 3.
For example, if you wish to compute the expression 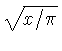 move the hairline over
move the hairline over 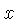 on
the CF or DF scale, and read the result on the W scale.
on
the CF or DF scale, and read the result on the W scale.
More generally, if you choose a number 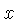 on a scale corresponding
to the function
on a scale corresponding
to the function 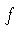 (as listed in Table 1), and you read the corresponding number
(as listed in Table 1), and you read the corresponding number 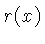 on a scale corresponding to the function
on a scale corresponding to the function 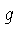 , then
, then
where 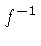 is the inverse function of
is the inverse function of
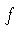 . The rows of tables 2 and 3 correspond to
. The rows of tables 2 and 3 correspond to 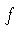 , and the
columns to
, and the
columns to 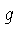 .
.
Note that
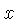 is not the number under the hairline on the C scale,
unless you choose to start on that scale!
is not the number under the hairline on the C scale,
unless you choose to start on that scale!
Table 2: One Variable Conversion
Table 3: More One Variable Conversion
There are some caveats about reading Tables 2 and 3. For example, 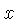 may have to be in a certain interval, and the tables do
not distinguish between different versions of the same scale, e.g.,
the various LL scales. For the S scale, we only consider the inverse
sine function, not the inverse cosine function. So before you use
your slide rule as suggested in the tables you'll have to think
carefully about what you are doing, which never hurts anyway. The
typesetting of some of those formulas is a bit idiosyncratic. They
were mostly machine generated, and I did not want to introduce
additional errors by excessive manual editing.
may have to be in a certain interval, and the tables do
not distinguish between different versions of the same scale, e.g.,
the various LL scales. For the S scale, we only consider the inverse
sine function, not the inverse cosine function. So before you use
your slide rule as suggested in the tables you'll have to think
carefully about what you are doing, which never hurts anyway. The
typesetting of some of those formulas is a bit idiosyncratic. They
were mostly machine generated, and I did not want to introduce
additional errors by excessive manual editing.
As the tables clearly indicate, if you move the hairline over any number
on any scale at all, and read the number on the same scale right under
the hairline, you'll get that very same number back!
Two Variables
Of course the number of possibilities is vastly increased by allowing
the slide to move. We consider two procedures, PLUS and MINUS,
involving scales 1, 2, and 3. Scales 1 and 3 are on the body, scale 2
is on the slide.
PLUS: Select u on scale 1 (on the body), align it with the index of
scale 2 (on the slide),
move the hairline to v on scale 2, and
read the result on scale 3 (on the body), underneath the hairline. For
example if the scales involved are D, C, and D, the
result would be the product, uv.
MINUS: Select u on scale 1, align it with v on
scale 2 on the slide, move the hairline to the index of scale 2, and
read the result on scale 3 on the body, underneath the hairline. For
example, if the scales involved are again D, C,
and D, the result is the quotient, 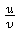 .
.
What happens if we use other scales? Assuming a (very hypothetical)
slide rule that has all the scales listed above both on the body and
on the slide, these two procedures let you evaluate 3,540 different
expressions in 4,394 different ways. Six examples are given in
Table 4.
Click here
to see a similarly organized pdf file (of
several hundred pages) showing all the possibilities.
In general, if 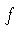 is the function corresponding to scale 1 (again, as listed in
Table 1),
is the function corresponding to scale 1 (again, as listed in
Table 1), 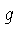 the function corresponding to scale 2, and
the function corresponding to scale 2, and 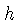 the
function corresponding to scale 3, then the result
the
function corresponding to scale 3, then the result 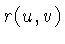 that you
read on scale 3 is
that you
read on scale 3 is
where the base of the logarithm is the length of the slide rule and
exp is the inverse function of log.
The symbol 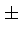 indicates whether to use the plus or the minus
procedure.
indicates whether to use the plus or the minus
procedure.
| row | entry | formula | variation | result | Scale 1 | Scale 2 | Scale 3 | +/- |
| 1 | 1 | 1 | 1 | 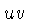 | CD | CD | CD | + |
| 2 | 15 | 2 | 1 | 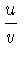 | CD | CD | CD | - |
| 3 | 2403 | 1803 | 1 | 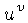 | LL | CD | LL | + |
| 4 | 139 | 26 | 2 | 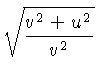 | CD | CDI | H | + |
| 5 | 287 | 83 | 1 | 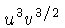 | CD | AB | W | - |
| 6 | 424 | 168 | 1 | 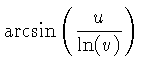 | CD | LL | S | - |
Table 4: Two Variable Computations
The first three rows of Table 4 show the most common operations on a
slide rule: product, quotient, and power.
The last three rows show less common formulas that can be evaluated.
Thus, according to the fourth row, to compute 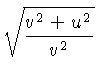 follow the PLUS procedure
with scales 1, 2, and 3 being D, CI, and H,
respectively. The first number in that row, 139, indicates the entry
in the pdf table, 26 means it is the 26th
distinct formula in the table, and 2 means it's the second way to
evaluate this particular formula. These numbers are not important for
the example, but they illustrate the organization of the pdf table.
Caveats apply even more so than to the one variable Table 2 and 3
above. The variables have to be in certain ranges, and you may have to
be judicious about which variant of the relevant scale you use to read
your result.
follow the PLUS procedure
with scales 1, 2, and 3 being D, CI, and H,
respectively. The first number in that row, 139, indicates the entry
in the pdf table, 26 means it is the 26th
distinct formula in the table, and 2 means it's the second way to
evaluate this particular formula. These numbers are not important for
the example, but they illustrate the organization of the pdf table.
Caveats apply even more so than to the one variable Table 2 and 3
above. The variables have to be in certain ranges, and you may have to
be judicious about which variant of the relevant scale you use to read
your result.
Of course, slide rule manuals do not list thousands of formulas. They
describe basic principles and then people can figure out how to use
slide rules to best advantage for their particular applications.
There are more pedestrian ways to compute 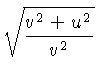 but if you have to evaluate
such expressions many times you'll find the shortcut eventually.
Once you have it you can impress your friends and coworkers!
but if you have to evaluate
such expressions many times you'll find the shortcut eventually.
Once you have it you can impress your friends and coworkers!
The last example in Table 4 requires an LL scale on the
slide. When I went to high school our work horse slide rule was the
Aristo Scholar 903. One version of it has a body and cursor with one
side, but a slide with two sides. The back of the slide shows several LL
scales. So prior to doing this calculation you need to turn the slide
around. This gives you a very strange slide rule without a C scale.
For years I have wondered for what kind of application one would want
to turn the slide on the Aristo Scholar, and after writing this web
page I know!
Three Variables
Suppose we consider a variant of the PLUS procedure where instead of
the index we use a number on a fourth scale. Thus we start again by
putting the hairline above the number u on scale 1. Then we
move the number v on scale 2 underneath the hairline. Next we
move the hairline above the number w on scale 3. Finally we
read the result on scale 4 underneath the hairline. Scales 1 and 4
are on the body, scales 2 and 3 on the slide. If the scales
are D, C, C, D respectively, the answer is
uw/v.
With the 13 scales assumed here, there are 24,314 distinct such
expressions, filling 2,143 printed pages that you can
view or download here. The four columns
following the mathematical expression give the scales 1, 2, 3, and 4
being used.
Sophisticated Multiplication and Division
Sophisticated Multiplication sounds like an oxymoron, but it
isn't in slide rule lore. We can multiply and divide using the
C and D scales, and so in particular we can multiply
with 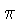 and compute reciprocals. Thus there is nothing we can
compute with the CI, DI, CF, DF,
CIF, and DIF scales that we can't compute with just the
C and D scales. The purpose of these additional scales
is to make multiplication and division fast and easy by minimizing the
number of times and the distances that the slide and cursor have to be
moved, particularly when doing repeated division and
multiplication. Try it, and you'll see that it is especially
convenient if multiplications and divisions alternate. If you have a
sequence of multiplications only you can replace some of them with a
division by the reciprocal of the relevant factor, using the
CI and DI scales. On the *F scales, the number
1 is almost exactly in the middle of those scales, and so by
switching to those scales when appropriate one can reduce the distance
by which one has to move the slide! If that was their only purpose,
the optimal folding factor for the *F scales would have been
the square root of 10. It so happens that
and compute reciprocals. Thus there is nothing we can
compute with the CI, DI, CF, DF,
CIF, and DIF scales that we can't compute with just the
C and D scales. The purpose of these additional scales
is to make multiplication and division fast and easy by minimizing the
number of times and the distances that the slide and cursor have to be
moved, particularly when doing repeated division and
multiplication. Try it, and you'll see that it is especially
convenient if multiplications and divisions alternate. If you have a
sequence of multiplications only you can replace some of them with a
division by the reciprocal of the relevant factor, using the
CI and DI scales. On the *F scales, the number
1 is almost exactly in the middle of those scales, and so by
switching to those scales when appropriate one can reduce the distance
by which one has to move the slide! If that was their only purpose,
the optimal folding factor for the *F scales would have been
the square root of 10. It so happens that 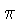 is close to that square root and works almost as well. In addition
however, it makes it possible to multiply or divide by
is close to that square root and works almost as well. In addition
however, it makes it possible to multiply or divide by 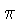 without any slide movement at
all. At some stage in the past someone had the quite brilliant idea
to approximate the square root of 10 by
without any slide movement at
all. At some stage in the past someone had the quite brilliant idea
to approximate the square root of 10 by 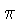 .
.
Quadratic Equations
As discussed above, one thing slide rules can do that calculators
can't is create tables. Here is an intriguing application of that
idea that I found in the Post Versalog Slide Rule Instructions,
Frederick Post Company, 1963. That readable little book describes very
many applications of slide rules.
Suppose we want to find the roots of the equation
Let's assume that 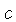 is positive, and the roots are
real. If
is positive, and the roots are
real. If 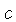 is negative we ignore that fact and worry
about the signs of the solutions later. As an exercise you may want
to figure out what happens when the roots of the quadratic equation
are complex. If the solutions are
is negative we ignore that fact and worry
about the signs of the solutions later. As an exercise you may want
to figure out what happens when the roots of the quadratic equation
are complex. If the solutions are 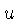 and
and 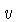 we have So we want to find two numbers
we have So we want to find two numbers 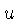 and
and
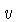 that add to
that add to 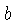 and multiply to
and multiply to 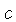 . We
move the hairline over
. We
move the hairline over 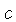 on the D scale, and
place the beginning or end of the slide under the hairline (choosing
whichever causes the smaller projection of the slide beyond the body).
Now the product of any pair of numbers on the D and CI
scales (or on the DF and CIF scales) is equal to
on the D scale, and
place the beginning or end of the slide under the hairline (choosing
whichever causes the smaller projection of the slide beyond the body).
Now the product of any pair of numbers on the D and CI
scales (or on the DF and CIF scales) is equal to 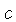 . Your slide rule now contains a table of pairs of numbers
that all have the same product. All that's left to do is to move the
hairline until we find a pair of numbers on the D and CI
scales (or DF and CIF scales) that add to
. Your slide rule now contains a table of pairs of numbers
that all have the same product. All that's left to do is to move the
hairline until we find a pair of numbers on the D and CI
scales (or DF and CIF scales) that add to 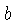 . Computing the sums mentally as we move the hairline is a
pleasant exercise that requires no external help. Once we have the
pair of numbers we can figure out the sign of the roots from the signs
of
. Computing the sums mentally as we move the hairline is a
pleasant exercise that requires no external help. Once we have the
pair of numbers we can figure out the sign of the roots from the signs
of 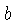 and
and 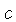 .
.
Cursor Marks
Many slide rules have special purpose marks on the cursors, in
addition to the hairline. As an illustration, here is a list of
calculations that can be accomplished with the cursor marks on the
Faber Castell Slide Rule pictured above.
- Put the hairline over the diameter of a circle on scale D
or C and read the area of the circle under a special mark on
scale A or B.
- The same marks can be used with the CI scale to compute the
volumes of cylinders.
- Two marks facilitate instant conversion of kW and hp (PS)
on the scales C and D.
- To multiply a number with 3.6 (and an integer power of 10)
put the hairline over it on the C or D scale, and read the
result under a special mark on the CF or DF scale. Of
course, reversing that procedure let's you divide by 3.6.
Specific Slide Rules
Table 5 lists scales on some specific slide rules. Numbers indicate
the number of scales present. For example, 8
LL scales usually means 8 distinct scales, 2 C scales
usually means there is a C scale on each side of the slide
rule. A green entry means the
scale is on the slide, a black it is on the body. Name is the
name of the slide rule.
Sides lists how many sides are used (one or both, or one and a
half in the case where the slide is reversible but there are no
scales on the back of the body).
Scales lists the total number of scales. The table is sorted
by decreasing total number of scales.
Marks lists how many marks are on the cursor, including the
hairline, and the remaining columns indicate the specific scales as
listed above. The last column gives reference numbers corresponding
to notes that follow the table.
| Name |
Sides |
Scales |
Marks |
C |
D |
CI |
DI |
CF |
DF |
CIF |
A |
B |
R,W |
K |
LL |
L |
S |
T |
ST |
P |
H |
Sh |
Ch |
Th |
Notes |
| |
| Pickett N4 |
2 |
33 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
|
|
2 |
|
8 |
1 |
1 |
2 |
1 |
|
|
2 |
|
1 |
9 |
| Aristo Hyperlog 0972 |
2 |
31 |
6 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
8 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
|
| Faber Castell Novo-Biplex 2/83 N |
2 |
30 |
11 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2,2 |
1 |
8 |
1 |
1 |
2 |
1 |
1 |
|
|
|
|
1,2 |
| Pickett N803 |
2 |
28 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
8 |
1 |
1 |
1 |
1 |
|
|
|
|
|
6,7 |
| Aristo MultiLog 0970 |
2 |
24 |
6 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
8 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
| Aristo Studio |
2 |
23 |
6 |
2 |
2 |
1 |
|
1 |
1 |
1 |
1 |
1 |
|
1 |
6 |
1 |
1 |
2 |
1 |
1 |
|
|
|
|
|
| Post Versalog |
2 |
23 |
2 |
2 |
2 |
1 |
|
1 |
1 |
1 |
|
|
2 |
1 |
8 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
| Faber Castell 52/82 |
2 |
22 |
7 |
2 |
2 |
1 |
|
1 |
1 |
1 |
1 |
1 |
|
1 |
3 |
1 |
1, 1 |
2 |
1 |
1 |
|
|
|
|
4 |
| Pickett N600 |
2 |
22 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
|
1 |
1 |
|
1 |
6 |
1 |
1 |
1 |
1 |
|
|
|
|
|
8 |
| Aristo Scholar 0903 LL |
1.5 |
15 |
4 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
3 |
1 |
1, 1 |
1 |
1 |
|
|
|
|
|
3,4 |
| Faber Castell 111/54 |
1.5 |
14 |
5 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
3 |
1 |
1 |
1 |
|
1 |
|
|
|
|
3,4,10 |
| Faber Castell 57/89 |
1.5 |
14 |
5 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
2 |
1 |
1,1 |
2 |
1 |
|
|
|
|
|
10 |
| Pickett Electronic N-515 |
1 |
11 |
1 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
|
|
|
2 |
1 |
1 |
|
|
|
|
|
|
13 |
| Aristo Scholar 0903 |
1 |
10 |
4 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|
| Pickett Trig Projection Rule |
1 |
9 |
1 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
|
1 |
1 |
1 |
|
|
|
|
|
|
12 |
| Pickett Microline 120 |
1 |
9 |
1 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
|
1 |
1 |
1 |
|
|
|
|
|
|
11 |
| Faber Castell Mentor 52/80 |
1 |
7 |
5 |
1 |
1 |
1 |
|
1 |
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
5 |
| Pickett Microline 160 |
1 |
7 |
1 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
| |
Table 5: Specific Slide Rules
Notes:
- The LL0 scale is merged with one of the D scales.
- The W scales enable multiplication and division with
increased accuracy, effectively providing a rule with a length of two
feet.
- The slide is reversible. The scales one the back side are
S, and 3 LL scales.
- One additional scale, labeled BI, shows
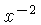 .
.
- Has rulers and instructions on the back of the scale.
- LL scales are merged with their reciprocals, e.g., LL1 with
LL01.
- Has a special DFM scale on the body. It is folded at
M which is the base 10 logarithm of e.
- Also has an Ln (natural logarithm) scale.
- Has the following additional scales:
- 3 cube root scales on the body
- A pair of scales folded about the base 10 logarithm of e.
- A natural logarithm scale on the slide.
- One edge of the slide rule protrudes and can be used as a ruler.
- This rule is available as part of a "programmed self instruction
kit". Also has instructions on the back of the rule.
- Is made of clear plastic to be used on an overhead projector, for
teaching purposes. Comes with a 48 page instruction manual.
Comes in a box labeled "All Metal Slide Rule".
- Fine example of a special purpose slide rule. Made for
electronic calculations specifically in the Cleveland Institute of
Electronics. Back Side has tables and formulas helpful in
electronics. There are two special purpose scales. One shows
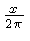 , the other shows
, the other shows 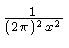 .
One L scale has base 10, the other base e.
.
One L scale has base 10, the other base e.
Home Work
I'm employed by an institution of higher learning, and I feel
compelled to assign some home work problems:
- Think about ways of making slide rules more accurate.
- Why is it that there seem to be no slide rules that have L
scales on both the slide and the body, thus enabling addition and
subtraction?
- Think carefully about the base of the logarithm used on a slide rule.
- Slide rules work because the logarithm of the product is the sum
of the logarithms. Could you use functions other than logarithms?
It's an excellent exercise to work out the answer, but if you can't or
won't, but you must know, click here!
- How do you solve a quadratic equation with complex roots, using your
slide rule?
- Build your own slide rule.


![]() ), and some explanations or comments.
), and some explanations or comments.
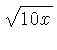 , and have a prime
attached to distinguish location on the body or slide.
These scales are labeled R
(Root) or W
(Wurzel). The radical symbol may also be used.
, and have a prime
attached to distinguish location on the body or slide.
These scales are labeled R
(Root) or W
(Wurzel). The radical symbol may also be used.
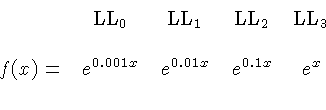
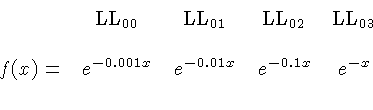
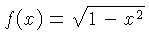
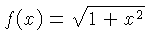
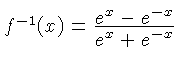
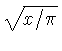 move the hairline over
move the hairline over ![]() on a scale corresponding
to the function
on a scale corresponding
to the function ![]() (as listed in Table 1), and you read the corresponding number
(as listed in Table 1), and you read the corresponding number ![]() on a scale corresponding to the function
on a scale corresponding to the function ![]() , then
, then ![]() is not the number under the hairline on the C scale,
unless you choose to start on that scale!
is not the number under the hairline on the C scale,
unless you choose to start on that scale!
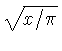
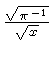
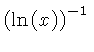
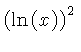
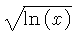
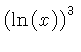
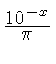
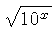
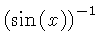
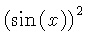
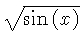
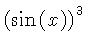
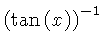

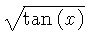

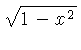
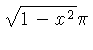
![$ \sqrt [4]{1-{x}^{2}} $](simg140.gif)
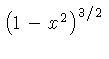
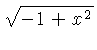
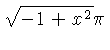
![$ \sqrt [4]{-1+{x}^{2}} $](simg152.gif)
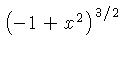
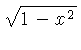
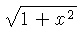
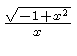
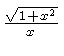
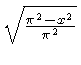
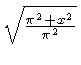
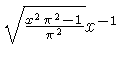
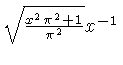
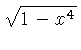
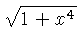
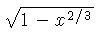
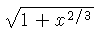
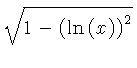
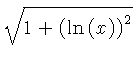
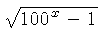
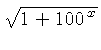
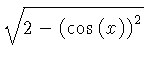
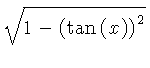
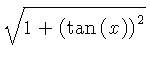
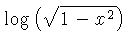
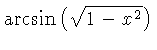
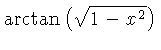
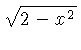
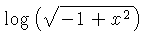
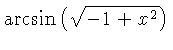
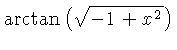
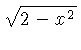
![]() .
.
![]() is the function corresponding to scale 1 (again, as listed in
Table 1),
is the function corresponding to scale 1 (again, as listed in
Table 1), ![]() the function corresponding to scale 2, and
the function corresponding to scale 2, and ![]() the
function corresponding to scale 3, then the result
the
function corresponding to scale 3, then the result ![]() that you
read on scale 3 is
that you
read on scale 3 is
![]() indicates whether to use the plus or the minus
procedure.
indicates whether to use the plus or the minus
procedure.
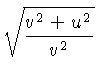
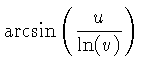
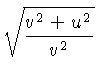 follow the PLUS procedure
with scales 1, 2, and 3 being D, CI, and H,
respectively. The first number in that row, 139, indicates the entry
in the pdf table, 26 means it is the 26th
distinct formula in the table, and 2 means it's the second way to
evaluate this particular formula. These numbers are not important for
the example, but they illustrate the organization of the pdf table.
Caveats apply even more so than to the one variable Table 2 and 3
above. The variables have to be in certain ranges, and you may have to
be judicious about which variant of the relevant scale you use to read
your result.
follow the PLUS procedure
with scales 1, 2, and 3 being D, CI, and H,
respectively. The first number in that row, 139, indicates the entry
in the pdf table, 26 means it is the 26th
distinct formula in the table, and 2 means it's the second way to
evaluate this particular formula. These numbers are not important for
the example, but they illustrate the organization of the pdf table.
Caveats apply even more so than to the one variable Table 2 and 3
above. The variables have to be in certain ranges, and you may have to
be judicious about which variant of the relevant scale you use to read
your result.
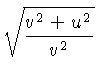 but if you have to evaluate
such expressions many times you'll find the shortcut eventually.
Once you have it you can impress your friends and coworkers!
but if you have to evaluate
such expressions many times you'll find the shortcut eventually.
Once you have it you can impress your friends and coworkers!