Configuration C11 of the 6-complex
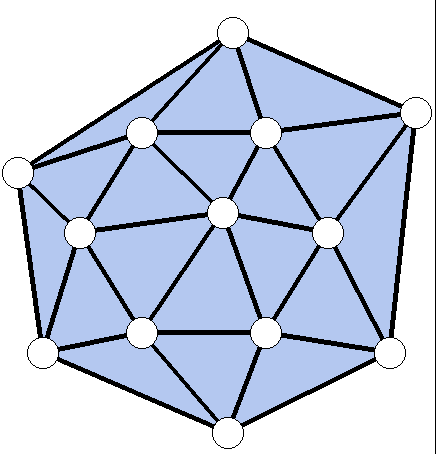
MDS: Version 4.33, 3/24/99 run # 2570
triangulation 4
13 Vertices
0: (230,280)
1: (149,400)
2: (273,400)
3: (335,300)
4: (273,200)
5: (149,200)
6: (87,300)
7: (235,500)
8: (397,420)
9: (423,180)
10: (240,100)
11: (25,240)
12: (50,420)
18 Triangles:
0: 0 1 2
1: 0 2 3
2: 0 3 4
3: 0 4 5
4: 0 5 6
5: 0 6 1
6: 7 1 2
7: 8 2 3
8: 9 3 4
9: 10 4 5
10: 11 5 6
11: 12 6 1
12: 2 7 8
13: 3 8 9
14: 4 9 10
15: 5 10 11
16: 6 11 12
17: 1 7 12
6 boundary edges:
0: 7 8
1: 8 9
2: 9 10
3: 10 11
4: 11 12
5: 7 12
24 interior edges:
0: 0 1 --- 2 6
1: 1 2 --- 0 7
2: 0 2 --- 1 3
3: 2 3 --- 0 8
4: 0 3 --- 2 4
5: 3 4 --- 0 9
6: 0 4 --- 3 5
7: 4 5 --- 0 10
8: 0 5 --- 4 6
9: 5 6 --- 0 11
10: 0 6 --- 5 1
11: 1 6 --- 0 12
12: 1 7 --- 2 12
13: 2 7 --- 1 8
14: 2 8 --- 3 7
15: 3 8 --- 2 9
16: 3 9 --- 4 8
17: 4 9 --- 3 10
18: 4 10 --- 5 9
19: 5 10 --- 4 11
20: 5 11 --- 6 10
21: 6 11 --- 5 12
22: 6 12 --- 1 11
23: 1 12 --- 6 7
6 boundary vertices: 7 8 9 10 11 12
7 interior vertices: 0 1 2 3 4 5 6
r = 1 d = 1
