
A Financial Calculator
The applet on this page let's you bring up a financial calculator
that
you can use to compute your loan payments, examine the evolution of your
savings, or plan your retirement.
The calculator let's you explore the connections between 5
financial parameters:
- n: the number of payments. These are usually monthly, but
could be any other time interval.
- The interest (p) in percent, paid per
payment.
Thus if you make monthly payments at an annual interest rate of 12%
p will equal 1%.
- The Principal Value, (PV). The amount of
money you borrow. Thus if PV is positive you take out a loan,
if PV is negative, you put money into your account to start
things off.
- Your regular payment, (pmt). Financial
calculators usually require that a payment you make is negative, but
to me a negative "payment" should mean you get money. Thus pmt
is positive when you pay off a loan, and it's negative when you draw
money out of an account.
-
The Future Value, (FV), of your investment. It is zero if you
simply pay off a loan, positive if you save a certain amount of money,
and negative if you are planning to pay off or refinance a balloon
payment at the end of your payment.
Examples
The menu below let's you look at several detailed examples showing the
calculator, a plot of the payment plan, and a detailed table of payments.
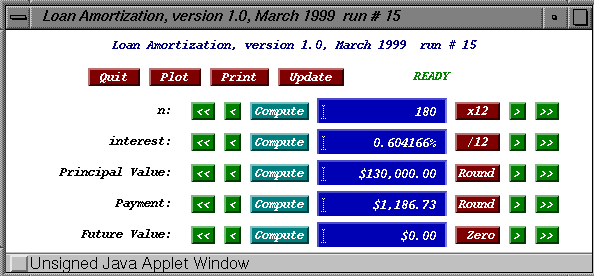
User's Guide
The image nearby shows what you should see on your screen after
clicking on the applet.
You need to specify the contents of four of the blue textfields
and then click on the button labeled compute next to the
fifth. The Calculator will compute the value of the fifth parameter
and display it in the corresponding text window. You can also print
or plot a payment plan.
Following is an explanation of the individual items on the
Calculator:
- Textfields The central ingredients of the Calculator are
the blue textfields. They let you enter Data and they display data.
To enter or modify data highlight the region ion the textfield you
want to change and type in the replacement. To make the program take
note of your change it is essential that you press the Enter or Return key.
- Compute Buttons For all financial parameters these cause
the calculator to compute the parameter in the same row so as to be
consistent with the other four parameters.
- Increment Buttons These green Buttons let you use
shortcuts to change the entries of the textfields. Their precise
effects are explained below. You don't need to type Enter in the
textfield after using one of the increment buttons.
- Red Buttons These have specialized effects explained below.
Let's now go through the rows and explain the features of each.
- Row 1. The run # is incremented by 1 every time the
Calculator is used.
- Row 2.
- Quit Clicking on this button causes the Calculator to
disappear. If you called it from the applet on this page you can make
it reappear by clicking on the applet. If you are using it in stand
alone mode you need to restart it.
- Plot This causes a very rudimentary plot to be drawn that
is explained in Example 1.
- Print This causes a listing of the payment plan. You can
see it ion the Java Console or in the window from which you started
the Calculator. Depending on your particular computing set up this
listing can be captured and put into a file.
- Update This button causes the contents of all textfields
to be set equal to the internal values kept by the calculator at that
time. Actually the textfields should be up-to date all the time and
so should need that button. But it's there so you can reassure
yourself if you have any doubts.
- Status Label Next to the buttons in this row there is a
label telling you the current status of the calculator:
- ready This means you can compute any of the five parameters
to make it consistent with the remaining four.
- consistent This means one of the parameters has been
computed, and the five values you see are consistent.
- did not parse The calculator did not understand what number
you just tried to tell it in one of the textfields.
- Floating Overflow The calculator tried to compute a number
that is too large to be expressed in its internal number system.
(That means its absolute value exceeds 10308.
- log of negative The calculator tried to compute the
logarithm of a negative number.
- no convergence The calculator failed to compute an interest rate.
- Row 3, n, the number of payments.
Small increments change that number by 1, large increments by 12.
(Think of 12 monthly payments being one yearly payment.) The Button
labeled x12 lets you enter the duration of the loan as a number of
years followed by converting that number to the number of months.
- Row 4, interest. This is the interest rate in percent per payment.
Small increments change the interest rate by 0.1, large ones by 1.
The button labeled /12 lets you enter an annual interest rate and
convert it to the monthly interest rate.
-
Row 5, Principal Value. A positive value indicates you have
money to spend, a negative value means someone made an
initial payment into your account. Small increments change the value by $1, large ones
by $1000. The Round Button rounds the Principal Value to the next
higher multiple of $1,000.
-
Row 6, Payment. A positive value indicates you pay money, a
negative one you receive money. Small increments change the payment
by $1.0, large ones by $10. The Round button rounds the payment to
next highest dollar.
-
Row 7, Future Value. A positive value indicates you have
money available after making payments, a negative value means you
still own money. Small increments change the value by $1, large ones
by $1000. The Zero Button sets the Future Value to zero.
The Mathematics
Since this is a mathematic page I'll have to tell you what's happening
inside the Calculator.
 (1)
(1)
Then it is a simple exercise to verify that the key equation
linking our five parameters is
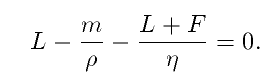 (2)
(2)
This equation can be solved explicitly for four of the five
parameters:
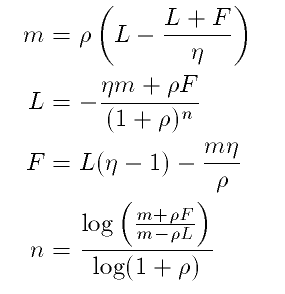 (3)
(3)
To solve (2) for p a simple numerical technique
(bisection) is used.
Downloading and Running Standalone
You can download this code and run it without a browser.
You need two files
Download the files and invoke Loan.class like you would any Java code. For example, on a Unix system you type
java Loan
Last change: [13-Mar-1999]
Copyright © 1998 Department of Mathematics,
University of Utah
 (1)
(1)


 (1)
(1)
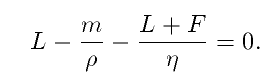 (2)
(2)
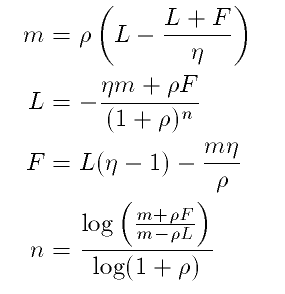 (3)
(3)