
Eratosthenes of Cyrene
A versatile scholar, Eratosthenes of Cyrene lived
approximately 275-195 BC. He was the first to estimate
accurately the diameter of the earth. For several decades,
he served as the director of the famous
library in Alexandria.
He was highly regarded in the ancient world, but
unfortunately only fragments of his writing have survived.
Eratosthenes died at an advanced age from voluntary
starvation, induced by despair at his blindness.
Here are some links to Eratosthenes related web pages:
The Sieve of Eratosthenes
Eratosthenes also conceived the "Sieve of Eratosthenes
", a method of identifying prime numbers. If you have
a
Java
compatible browser you can use that sieve right here, from
this Applet:
What is the Sieve of Eratosthenes?
A
prime number
is a natural number greater than 1 that can be divided
without remainder only by itself and by 1. Natural
numbers n that can be divided by a number less
than n and greater than 1 are composite
numbers. The Sieve of Eratosthenes
identifies all prime numbers up to a given number n
as follows:
-
Write down the numbers 1, 2, 3, ..., n. We will
eliminate composites by marking them. Initially all
numbers are unmarked.
-
Mark the number 1 as special (it is neither prime
nor composite).
-
Set k=1. Until k exceeds or
equals the square root of n do this:
-
Find the first number in the list greater
than k that has not been identified as
composite. (The very first number so found
is 2.) Call it m. Mark the numbers
2m, 3m, 4m, ...
as composite. (Thus in the first run we
mark all even numbers greater than 2. In
the second run we mark all multiples of 3
greater than 3.)
-
m is a prime number. Put it on
your list.
-
Set k=m and repeat.
Put the remaining unmarked numbers in the sequence
on your list of prime numbers.

This is exactly what the applet does. If the natural
numbers are arranged in a rectangular array than marking
the composites gives rise to interesting patterns. The
Figure nearby shows one of these patterns (the prime
numbers from 2 through 12,743), but seeing the pattern
develop is much more interesting than seeing the static
final result. Experiment with various options yourself!
Click here or on the pattern
to see a similar pattern made of boxes 2 by 2 pixels
large, forming a 529 by 369 rectangle, and showing all
primes up to and including 195197.
Since this is an educational page I'll give you a home
work problem: Explain the vertical streaks that seem
to be present in the pattern. Once you are done with
that, explain why there are no horizontal streaks!
Send me your answer!
The remainder of this page is
A User's Guide to the Sieve of Eratosthenes Applet
A quick tour
To see how it works, do the following:
-
Click on the applet. Two windows, called "
Sieve of Eratosthenes Controls" and "The
Sieve of Eratosthenes" will pop up on your
screen. They should look like the images nearby on
this page and fit on your screen. Arrange them
conveniently so that you can see both windows
without obstruction. Let's call them the
control panel and the drawing window.
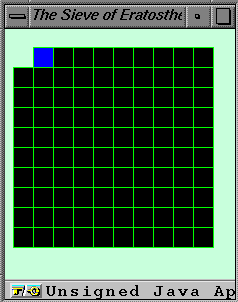
The boxes in the drawing window should form a 10 by
10 array representing the numbers 0 through 99
arranged as we read (i.e., from the top left corner
to the bottom right corner). Check you
understanding by clicking on some of the black boxes
and seeing the corresponding numbers show up in the
textfield labeled pick: in the 3rd row of
the control panel. The blue box corresponds to 1,
which as we saw is different from all other numbers.
The number zero is not shown since it isn't a
natural number.
-
Move the cursor into the drawing window and hit the
key "s" (for "step"). The
square corresponding to the number 4 is colored
white. That means it is not a prime number (since
it is a multiple of 2). Hit "s" again.
The number six square is colored white. Do this a
few times until you see what's happening.
-
Hit the key "p" (for "prime").
The multiples of 2 will be finished off.
-
Hit "s" again (or "p") to see
what happens to the multiples of 3.
-
Hit "a" (for "all") to see the
rest of the process. The prime numbers from 2 to
100 are now marked with black boxes. Click on some
of them to see that they do indeed correspond to the
prime numbers.
-
In the second row of the control panel, change the
number in the textfield labeled "size" to
2. (To do this, highlight the 20 that's in the
field, type 2, and hit return.) Then click on "
do it all" in the first row of the control
panel. You'll see patterns emerge as the Sieve of
Eratosthenes proceeds, and the final picture (if you
didn't resize the drawing window) should look like
the pattern in the image above..
-
If the process is too slow for your taste, do this:
-
Click on "reset" in the control
panel.
-
Change "Delay" in the second row
of the control panel to 0.
-
Click on "Do it all".
-
If this is still not fast enough, select
" Fast" in the upper right corner
of the control panel, click on "reset
", and click on "do it all"
again. Now the sieve will run as fast as it
can on your machine.
Details of the Operation.
To Start
Starting is very simple. You click on the applet.
To Quit
Quitting is also very simple. It can be accomplished in
a number of ways:
-
Click in the applet on your web page.
-
Click on the QUIT button in the control
panel.
-
Type "x", "X", "Q", or
"q" in any window.
-
Quit your browser.
The Control Panel
Let's run through the rows of the control panel:
-
Row 1.
-
do it all! This button starts the
sieve, which will run to completion (unless
it is interrupted).
-
do 1 prime will start the sieve and
let it run until the multiples of the
current prime are all marked. If the button
is clicked during a full run (started by
do it all! ) the run will stop after the
current prime is completed.
-
do 1 step similarly will take 1 step
of the sieve and then cause it to stop. It
will also stop a run in progress.
-
reset will return the drawing window
to its original state.
-
resize is required for one of the
methods for resizing the drawing window. To
use it, resize the drawing window manually
and then click on it.
-
The safe/fast menu will select the
safe or fast mode. In the fast mode the
program runs a little faster and uses less
memory. In the safe mode you can partially
cover and uncover, or even close and reopen,
the drawing window and its contents will be
restored.
-
Row 2.
-
Size: This is the size (in pixels) of
the square corresponding to the numbers 1,
2, ... . Changing the size will also cause
the drawing window to be reset. The minimum
possible size is 1. If the size is greater
than 4 then each square is surrounded by a
green outline. Altering the size will
increase or decrease the n but not
the size of the drawing window.
-
Delay: This is the delay in
milliseconds used when marking a number as
composite. During the delay the
corresponding square is rendered in red.
For large investigations the delay should be
set to zero, but for demonstrations larger
values may be suitable.
-
Row 3
-
Primes: The text window with the
buttons "-" and "+" next
to it displays the primes that have been
found. By default the largest one is
displayed. You can go up and down in the
list by clicking on the "-" and
"+" buttons, respectively.
Overwriting the number in the text field
will cause the next largest prime to be
displayed (within the range of primes found
by the sieve).
-
pick: Clicking on one of the squares
in the drawing window will cause the
corresponding number to appear in the text
field. This is useful for orienting
yourself.
-
Row 4. The text windows give the horizontal
and vertical extents extent of the drawing window
(in boxes) and the length of the list used in the
sieve. You can resize the drawing window by
specifying the horizontal and vertical extents in
the text windows.
-
Row 5. I increase the version number whenever
there is a significant change in the code, by an
amount roughly proportional to the change. If you
are using an old version then you should probably
replace it with the newer version provided here (see
the downloading instructions below). The Run #
is the total number of runs since November 1,
1996, by all copies of the program, to date. I'm
not trying to spy on you, but I am curious how much
the program is used, and I'm also fascinated by the
technology. The count is obtained by sending an
inquiry to my system which returns the current
count. This ability to communicate over the net
opens a lot possibilities which are as yet not even
recognized. If my server daemon is down the program
runs fine without indicating a count.
The Drawing Window
You can resize the drawing window in several ways:
-
Change the horizontal or vertical extent of the
drawing area in the control panel. This will
interrupt any drawing in progress.
-
While no drawing is in progress, change the
size of the window manually, and then click on
"resize ".
You can also control the drawing action via the key
board as follows:
-
"a" or "A" are the equivalent of
do it all!
-
"p" or "P" are the equivalent of
do 1prime
-
"s" or "S" are the equivalent of
do 1 step
-
"r" or "R" are the equivalent of
reset
-
"d" or "D" set the delay equal
to zero and accelerate the drawing.
-
"x", "X", "q" or
"Q " are the equivalent of quit
Getting the most out of your applet.
To compute the largest possible range of primes on your
machine do the following:
-
Click on "reset" or otherwise make sure
the drawing has stopped.
-
Set "size" to 1.
-
Make the drawing window as large as possible, and
lower the window, or close it.
-
Click on "resize".
-
Set the delay to zero and click on "do it all!
", or with the cursor in the drawing window
type "d" and "a".
On my machine this process gives rise to a window that
1254 by 894, with n=1,121,075..
Running Standalone and Downloading
You may download the byte code of this software and
incorporate it into your own web pages or run it on your
system in a standalone mode. You need the following
Java classes:
When you click on these links (which point to binary
files) you'll probably see something strange on your
system. However, you should be able to download the
files properly in spite of their appearance.
Sieve is the class that calls all others. To run
the software in standalone mode on a Unix system just
type java Sieve in the directory that contains
your class files. If you want to base an Applet on your
files make sure you specify the code base (the directory
containing your class files) similarly as in the html
code of this page. The code base must be accessible
over the net, otherwise you get a security exception and
things don't work right.
If you do download the software I invite you to
let me know
so that I can put you on my mailing list and inform you
about future improvements. Of course, also let me know
if you have any troubles.
There is no help information built into the program (at
least not yet). This page is intended to be the
documentation for the program. So you may want to copy
the page, print it, or provide a link to it.
Known Bugs
This is a list of known bugs. I'm working on them, but
at the moment it's not clear to me how to find and
correct them (otherwise I'd fix them immediately). If
you have any suggestions, or would like to report other
bugs, please
write to me!
-
Some actions during the drawing process cause the
computation to go faster, but at the expense of
resisting interruption, and omitting to repaint the
drawing window after covering or closing it. These
actions include resizing the drawing window or and
clicking somewhere in the drawing window. Until
this bug is fixed, perhaps you can look at it as a
feature!
[02-Jun-1998]
Return to Peter Alfeld's Home Page.




