
The N by N Queens Problem
In chess, a queen can move as far as she pleases,
horizontally, vertically, or diagonally. A chess board has
8 rows and 8 columns. The standard 8 by 8 Queen's problem
asks how to place 8 queens on an ordinary chess board so
that none of them can hit any other in one move.

Besides being an amusing puzzle this problem is interesting
because kids love it and it's a great teaching tool in the
upper grades of Elementary School. It also provides great
programming exercises.
One solution - the prettiest in my opinion - is given in the
figure nearby. It turns out that there are 12 essentially
distinct solutions. (Two solutions are not essentially
distinct if you can obtain one from another by rotating your
chess board, or placing in in front of a mirror, or
combining these two operations.)
Even though the solution shown here looks pretty natural and
straightforward, it is not that simple to find any others,
or even this one if I hadn't displayed it here. As an
exercise you may want to find the other solutions. If you
are impatient, you can look them up by
clicking here.
Our particular solution is configuration 10.
An obvious modification of the 8 by 8 problem is to consider
an N by N "chess board" and ask
if one can place N queens on such a board. It's
pretty easy to see that this is impossible if N is
2 or 3, and it's reasonably straightforward to find
solutions when N is 4, 5, 6, or 7. The problem
begins to become difficult for manual solution precisely
when N is 8. Probably the fact that this number
coincidentally equals the dimensions of an ordinary chess
board has contributed to the popularity of the problem.
The interactive applet on this page let's you find solutions
of the N by N Queen's Puzzle for arbitrary
values of N. You may find it interesting to watch
your computer find the solutions.
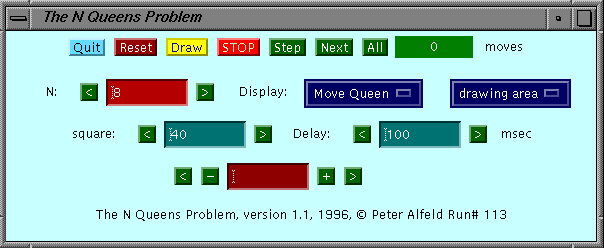
When you first click on the applet you should see a control
panel looking just like this one (which is an ordinary gif
image - clicking on it will not accomplish
anything.) You should also see a drawing frame that contains
an 8 by 8 chess board much like the one exhibiting the
example solution above. You can use the applet to compute
more solutions at various levels of animation (and
correspondingly reduced levels of speed).
The Algorithm
The program finds solutions by starting with a queen in the top
left corner of the chess board. It then places a queen in the
second column and moves it until it finds a place where it
cannot be hit by the queen in the first column. It then places
a queen in the third column and moves it until it cannot be hit
by either of the first two queens. Then it continues this
process with the remaining columns. If there is no place for a
queen in the current column the program goes back to the
preceding column and moves the queen in that column. If the
queen there is at the end of the column it removes that queen as
well and goes to the preceding column. If the current column is
the last column and a safe place has been found for the
last queen, then a solution of the puzzle has been found. If
the current column is the first column and its queen is being
moved off the board then all possible configurations have been
examined, all solutions have been found, and the algorithm
terminates.
When a solution has been found it can be displayed in its
own window. Currently the program does not eliminate
solutions that can be obtained from previous ones by
rotations or reflections.

A measure of the difficulty of the problem is given by the
number of moves the above algorithm takes to find the
first solution. This number of course tends to go up as
as N increases, but it does not increase
monotonically. The Table nearby gives the required number
of steps. It is ordered by increasing difficulty. So the
easiest board to find a solution on is the 5 by 5 board, and
the 22 by 22 board is about 65 times as hard as the 23 by 23
board, and about 41,000 times as hard as the 8 by 8 board.
Using the Control Panel
Let's run through the rows of the Control Panel:
-
Row 1.
-
Naturally, the Quit button lets you quit
the program. You can also exit by clicking
again on the applet, by typing 'x', 'X', 'q', or
'Q' in the control window, or by quitting your
browser. You can dismiss a single solution or
the drawing window by typing 'x', 'X', 'q', or
'Q' in the relevant window. (If you dismiss the
drawing window accidentally and you want it back
use the Draw button, see below.)
-
The Reset button stops any computation in
progress and resets the board to the initial
configuration with a single queen in the upper
right corner.
-
The Draw Button redisplays the Drawing
window if it has been previously dismissed. It
also updates the display of the current
configuration in the drawing window, and the
display of the step count on the control panel.
-
The STOP button interrupts any
computation in progress, but it does not reset
the board.
-
The green
buttons Step, Next and All
let you find more solutions. Step moves a
queen in the current configuration, Next
finds the new solution, and All finds all
solution. Caution: Using the All
button with each solution displayed on a new
board can fill your screen very quickly with new
windows showing new solutions and cause your
system to run out of memory or into some other
limit. For every new solution the program
pauses for the time indicated in the delay Text
Field. This gives you a chance to type 's' or
'S' in any displayed solution, which will stop
the production of new solutions. The control
window will also stay on top of the solution
windows so that you can stop or quit.
-
The text label shows the number of moves made so
far on the board. It is
green when the program is waiting
for your instructions, and
red when it's working on a
computation.
-
Row 2.
-
The red
textfield let's you change the value of N
, the dimension of the chess board. You
can decrease or increase N by clicking
on the "<" or ">"
button, respectively.
-
The Display Menu let's you determine the
degree of animation on the drawing board. There
are four levels, ordered by decreasing animation
and increasing speed:
-
Demonstrate shows queens being
moved, and has a ghost queen move from
any queen that can hit the recently
moved queen in the rightmost column.
-
Show: Queens that can hit each
other are rendered in grey.
-
Move Queen: The queens move, but
there is no indication which can be hit.
This is the default setting.
-
Results only Only new solutions
are displayed (in their own windows or in the
drawing window).
-
Row 3. The Text Field labeled square shows
the size of the chess squares (in pixels). You can
change that number to adjust to larger or smaller values
of N. The green "<" and "
>" buttons decrease or increase the square size
by 1. The delay in milliseconds is applied during any
animation. The "<" and ">"
buttons decrease or increase the delay by approximately
20 percent. Choosing 'Result only' in the display menu
causes the delay to be applied only when a board with a
new solution is being displayed.
-
Row 4. This row lets you display all distinct
solutions for N=4, 5, 6, 7, 8, and 9,
and the first solution found by the algorithm for values
of N larger than 9. The menu let's you decide
whether you want to see each solution in the general
drawing area (the default) or in its own display. (This
setting also applies to solutions found by the program
by searching.) The plus and minus buttons let you scroll
up and down the list for a given value of N.
You can also change the value of N by using the
"<" or ">" buttons. To get
any display click on plus or minus, or type a return in
the text field.
-
Row 5. As usual, I update the version number
whenever there is a significant change. The run number
indicates how often the program has been run since
November 30, 1996.
Running Standalone and Downloading
You may download the byte code of this software and incorporate
it into your own web pages or run it on your system in a
standalone mode. You need the following Java classes:
When you click on these links (which point to binary files)
you'll probably see something strange on your system.
However, you should be able to download the files properly
in spite of their appearance.
Queens is the class that calls all others. To run
the software in standalone mode on a Unix system just type
java Queens in the directory that contains your
class files. If you want to base an Applet on your files
make sure you specify the code base (the directory
containing your class files) similarly as in the html code
of this page. The code base must be accessible over the
net, otherwise you get a security exception and things don't
work right.
If you do download the software I invite you to
let me know
so that I can put you on my mailing list and inform you
about future improvements. Of course, also let me know if
you have any troubles.
There is no help information built into the program. This
page is intended to be the documentation for the program.
So you may want to copy the page, print it, or provide a
link to it.
Notes
-
The main point of the applet on this page is to
illustrate the computer search. However, given any size
chessboard it is possible to find a solution without
searching.
Click here for an illustration.
[03-Sep-1997]
Return to Peter Alfeld's Home Page.




